Engineering Need help about the magnetic field near an infinite current sheet

[e0ne199]

Homework Statement

hello everyone, i have a question about magnetic field from infinite current sheet...

Relevant Equations

the equation will be related with the application of Ampere's Law on current sheet

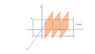
here is the question, don't mind about point (a) and (b) because i have solved them already...the main problem is the question on point (c) :

so far, what i have done is : H = 2.7*0.1-(1.4*0.15+1.3*0.25) = -0.265 a_z A/m which is the wrong answer compared to the solution provided from the question...any help is really appreciated, thanks before

 

[BvU]

what i have done is

I don't see the y-coordinate of $P$ in your version ?

 

[Henryk]

Use Ampere's law $\oint \vec H d \vec l = I$ twice. Use a rectangular path (which have to be in the plane perpendicular to the current direction). The first one would have to include pieces of all three current planes; this would give you the field on both sides of the stack of planes. The second one would have to go through your test point P.

 

[e0ne199]

Use Ampere's law $\oint \vec H d \vec l = I$ twice. Use a rectangular path (which have to be in the plane perpendicular to the current direction). The first one would have to include pieces of all three current planes; this would give you the field on both sides of the stack of planes. The second one would have to go through your test point P.

sorry for the late response, but do you know how to apply your solution to my problem? probably i still have a little understanding for this kind of question...please help

 

[e0ne199]

I don't see the y-coordinate of $P$ in your version ?

could you please point out which is wrong on my current answer?

 

[e0ne199]

hallo, anyone?

 

[BvU]

could you please point out which is wrong on my current answer?

Did you read the replies ?

hallo, anyone?

Instant service required after two weeks of silence? Still nice to hear back from you

the equation will be related with the application of Ampere's Law

what i have done is : H = 2.7*0.1-(1.4*0.15+1.3*0.25) = -0.265 az A/m

Yes, Ampere's law. As @Henryk wrote. It involves a path (maybe even several paths). Where is your path ? Is P on that path ?

 

[e0ne199]

Did you read the replies ?
Instant service required after two weeks of silence? Still nice to hear back from you
Yes, Ampere's law. As @Henryk wrote. It involves a path (maybe even several paths). Where is your path ? Is P on that path ?

i am sorry, i really don't understand about your clue...i did try to find another example for a whole week after posting that question here... the possible way i could think of is like this :

(2.7-1.4) X a_y = 1.3 a_z A/m but i am not sure if the way i get the answer is right or not...

 

[BvU]

really don't understand about your clue

But do you understand what I am asking ? Ampere <--> path . Where is your path ?

(2.7-1.4) X ay = 1.3 az A/m

What is X ? What are you doing here and how is it related to Ampere's law ?

 

[e0ne199]

But do you understand what I am asking ? Ampere <--> path . Where is your path ?

What is X ? What are you doing here and how is it related to Ampere's law ?

ok, here is the path, P is the green one, and pink line is the path.

about this

(2.7-1.4) X ay = 1.3 az A/m

i was doing a calculation with cross product, but i am not sure if this is the right way to do, since

H=K X a_n

so please tell me if i am doing it wrong or not

 

[Henryk]

oops, sorry, I have a symbol missing in Ampere's law, it should be $\oint \vec H \cdot \vec l = I$, i.e. dot product, not cross product and I is the total current enclosed by the loop with the direction given by the right hand rule.
Now, you notice that you can move vertical vectors left or right (i.e. changing the length of the horizontal vectors, portions of the path) and as long as they don't cross current planes, the enclosed current remains the same. This tells you $H_y = 0$. Similarily, the loop can be moved up or down and, since the current density is constant, the $H_z = const$
Now, consider the two loops, ABCD and FBCE and you should get the correct answer.

 

[BvU]

@e0ne199 : Isn't it wonderful what a clear picture can do !

 

[e0ne199]

oops, sorry, I have a symbol missing in Ampere's law, it should be $\oint \vec H \cdot \vec l = I$, i.e. dot product, not cross product and I is the total current enclosed by the loop with the direction given by the right hand rule.
Now, you notice that you can move vertical vectors left or right (i.e. changing the length of the horizontal vectors, portions of the path) and as long as they don't cross current planes, the enclosed current remains the same. This tells you $H_y = 0$. Similarily, the loop can be moved up or down and, since the current density is constant, the $H_z = const$
Now, consider the two loops, ABCD and FBCE and you should get the correct answer.

based on the diagram, the result is like this :

$H_z * l = K * l$
$H_z =$(loop ABCD)+(loop FBCE) = (2.7-1.4-1.3) + (-1.3) = -1.3 $a_z$ A/m

is that result correct?

 

[e0ne199]

umm.. hello, anyone?