Need help interpreting a spring-block problem

[tellmesomething]

Homework Statement

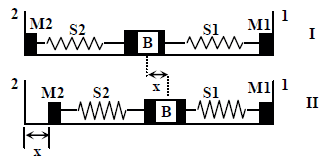
A block (B) is attached to two unstretched springs S1 and S2 with spring constants k and 4k, respectively (see fig 1). The other ends are are attached to identical supports M1 and M2 not attached to the walls. The spring and supports have negligible mass. There is no friction anywhere. The block B is displaced towards wall 1 by a small distance x (fig 1) and released. The block returns and moves a max distance y towards wall 2. Displacements x and y are measured with respect to equilibrium position of the block B. The ratio y/x is:

Relevant Equations

None

I haven't tried anything yet as im stuck at interpreting what the question asks itself.
Firstly the only force acting on M1 support is the spring force (kx) why did it not move?
Secondly is the reason of it not moving the fact that is also pulling the string with the same force (kx) so it is returning to its position against the wall?
I might have more questions as these get cleared sorry for the inconvenience :(

 

[BvU]

Posting the picture might be useful

And posting a best effort is mandatory in PF

$\$

 

[tellmesomething]

Posting the picture might be useful

And posting a best effort is mandatory in PF

$\$

I edited it just a minute later sorry the pic is up and running

 

[PeroK]

Firstly the only force acting on M1 support is the spring force (kx) why did it not move?

Where's it going to move? Through the wall?

 

[tellmesomething]

Where's it going to move? Through the wall?

The spring force acts forward I.e in the direction opposite to the applied force right? So wouldn't the spring be pulling on the support M1 instead of pushing it as you say.

 

[PeroK]

The spring force acts forward I.e in the direction opposite to the applied force right? So wouldn't the spring be pulling on the support M1 instead of pushing it as you say.

Spring S1 is compressed.

 

[PeroK]

M1 is being pushed into the wall, not pulled away from it.

 

[tellmesomething]

M1 is being pushed into the wall, not pulled away from it.

Spring S1 is compressed.

Yes but the point of application of force is the point connecting the head of the spring and the block B, the head of the spring gets compressed and produces a spring force equal to the extension times , in the opposite direction. Is it not the latter force which acts on the support M1?

 

[PeroK]

Yes but the point of application of force is the point connecting the head of the spring and the block B, the head of the spring gets compressed and produces a spring force equal to the extension times , in the opposite direction. Is it not the latter force which acts on the support M1?

Yes, but that force pushes M1 into the wall. A compressed spring is not going to pull M1 away from the wall.

If you pulled B in the opposite direction (to the left) that would extend the spring and pull M1 away from the wall.

 

[tellmesomething]

Yes, but that force pushes M1 into the wall. A compressed spring is not going to pull M1 away from the wall.

If you pulled B in the opposite direction (to the left) that would extend the spring and pull M1 away from the wall.

I dont think I explained really well this is what I meant, I just dont get how the external force is transmitted through the spring, I thought the reaction force or the spring force is responsible for transmitting the external force to the block.

 

[PeroK]

I dont think I explained really well this is what I meant, I just dont get how the external force is transmitted through the spring, I thought the reaction force or the spring force is responsible for transmitting the external force to the block.View attachment 342307

That's not how a spring works.

 

[tellmesomething]

That's not how a spring works.

Can you share a link or something where I can read more about this, I tried scouring the internet I didnt find much.

 

[PeroK]

Can you share a link or something where I can read more about this, I tried scouring the internet I didnt find much.

https://prohands.net/collections/frontpage/products/gripmaster

 

[tellmesomething]

https://prohands.net/collections/frontpage/products/gripmaster

Sorry, is that relevant?

 

[PeroK]

Sorry, is that relevant?

That's a product that's based on the property of a compressed spring pushing out in both directions. The people who designed it understood that. It's as good an example as any, as far as I can see. Or, do you think physics has nothing to do with the real world of real springs and real commercial products?

 

[tellmesomething]

That's a product that's based on the property of a compressed spring pushing out in both directions. The people who designed it understood that. It's as good an example as any, as far as I can see. Or, do you think physics has nothing to do with the real world of real springs and real commercial products?

No I think you misunderstood. I meant an article or source which explains how springs work..but I understand you're not obliged to do that. I'll look more. Sorry.

 

[PeroK]

No I think you misunderstood. I meant an article or source which explains how springs work..but I understand you're not obliged to do that. I'll look more. Sorry.

Physics is an empirical science. An object that you can experiment on is better in many ways than a theorectical article.

You need to think seriously about why I pointed you at a real, physical object that exhibited the property you do not understand. And, think seriously about why you reject that as a means of learning about physics.

 

[tellmesomething]

Physics is an empirical science. An object that you can experiment on is better in many ways than a theorectical article.

You need to think seriously about why I pointed you at a real, physical object that exhibited the property you do not understand. And, think seriously about why you reject that as a means of learning about physics.

I understand but I cannot have the physical object with me right now. I can watch tutorials which might broaden my understanding so i'll try that. In any case thankyou for the help. :)

 

[tellmesomething]

Physics is an empirical science. An object that you can experiment on is better in many ways than a theorectical article.

You need to think seriously about why I pointed you at a real, physical object that exhibited the property you do not understand. And, think seriously about why you reject that as a means of learning about physics.

I think ive made some progress with this and the question. So what ive gathered from spring mechanism is that S1 the string being compressed is also applying a force pushing the support into the wall and at the same time theres a restoring force which is equal to the external force which is being applied on the block . This i concluded because the spring S2 has not deformed which means there is a net zero force on it.

When the external force is removed, i.e when it is released from rest, theres a net acceleration in the direction of wall 2 because of the restoring force which cause block B to get back to its equilibirum position and since it was accelerating, it still has velocity in the direction of wall 2 and it moves compressing spring S2 till it reaches v=0 making it the maximum displacement of the blcok where theres momentary rest.

 

[PeroK]

I think ive made some progress with this and the question. So what ive gathered from spring mechanism is that S1 the string being compressed is also applying a force pushing the support into the wall and at the same time theres a restoring force which is equal to the external force which is being applied on the block . This i concluded because the spring S2 has not deformed which means there is a net zero force on it.

When the external force is removed, i.e when it is released from rest, theres a net acceleration in the direction of wall 2 because of the restoring force which cause block B to get back to its equilibirum position and since it was accelerating, it still has velocity in the direction of wall 2 and it moves compressing spring S2 till it reaches v=0 making it the maximum displacement of the blcok where theres momentary rest.

That's a reasonable summary. Note that the initial diagram is misleading as it shows both springs compressed. However, the problem statement implies that only S1 is compressed.

 

[kuruman]

Note that the initial diagram is misleading as it shows both springs compressed. However, the problem statement implies that only S1 is compressed.

In the top figure (I) we have to assume that both springs are at their equilibrium lengths as stated. The bottom figure (II) shows the mass displaced by $x$ to the right and the end of spring S2 also displaced to the right by $x$. Therefore, in the bottom figure S2 is at its equilibrium length. It looks like the springs are just drawn inconsistently from (I) to (II).

 

[tellmesomething]

That's a reasonable summary. Note that the initial diagram is misleading as it shows both springs compressed. However, the problem statement implies that only S1 is compressed.

Yes. Though im facing another unexpected problem. We know that net work done= Change in kinetic energy ? So work done in bringing the block from the x position to mean position is -0.5kx^2 and work done in bringing the block from mean position to the y compressed position is -2ky^2. If we apply the above formula and equate it to 0 then we get the ratio y/x in negative which is obviously wrong....where am i going wrong here?

 

[PeroK]

If we apply the above formula and equate it to 0 then we get the ratio y/x in negative which is obviously wrong....where am i going wrong here?

Why is that wrong?

 

[tellmesomething]

Why is that wrong?

I see..it does say displacement so it could be negative.
But this is a mcq question and all the options provided are positive

 

[tellmesomething]

In the top figure (I) we have to assume that both springs are at their equilibrium lengths as stated. The bottom figure (II) shows the mass displaced by $x$ to the right and the end of spring S2 also displaced to the right by $x$. Therefore, in the bottom figure S2 is at its equilibrium length. It looks like the springs are just drawn inconsistently from (I) to (II).

Thankyou

 

[PeroK]

I see..it does say displacement so it could be negative.
But this is a mcq question and all the options provided are positive

Is that an unsolvable problem?

 

[tellmesomething]

Why is that wrong?

also i would get something like -1/4=y^2/x^2 so i would have to take out the square root of a negative number to get y/x

 

[tellmesomething]

Is that an unsolvable problem?

?

 

[PeroK]

also i would get something like -1/4=y^2/x^2

That's definitely wrong.

 

[tellmesomething]

That's definitely wrong.

Yes.

 

[TSny]

So work done in bringing the block from the x position to mean position is -0.5kx^2

Why would this work be negative?

 

[tellmesomething]

Why would this work be negative?

Oh. That was really stupid. Thankyou very much. Also thankyou @PeroK for enduring this throughout and giving me new insights.

 

[PeroK]

Oh. That was really stupid. Thankyou very much. Also thankyou @PeroK for enduring this throughout and giving me new insights.

First, the problem explicitly says that $x$ and $y$ are distances. They are both positive.

Second, the system starts with some PE, which we take to be positive (relative to zero at equilibrium) and ends with PE, which must also be positive (relative to zero at equilibrium). It's not the case that one PE is positive and the other negative. The mass has positive PE at the start position and positive PE at the final position.

That second observation comes from a physical understanding of the problem. And, that physical understanding should determine how you set up your equations.

I would have simply equated:
$$PE_1 = PE_2$$
$$\implies \frac 1 2 k_1 x^2 = \frac 1 2 k_2 y^2$$And not given it a second thought. That must be the correct equation. If you asked me to fully justify that by applying the work-energy theorem rigorously at every step, then I'd have to be careful about negatives. But, I can't see any reason to complicate this problem.

 

[BvU]

I can't see any reason to complicate this problem

I have a nagging feeling, nevertheless. Block B is released and S1 starts to decompress, transferring spring energy that is converted to kinetic energy of block B plus spring energy from the compression of S2 plus kinetic energy of block M2.

At the moment when block B is passing its original position ('$y=0$'), there is also a part of the energy converted to energy to stretch spring S1 (which we know to be at its natural length at that point), plus kinetic energy of M1.

$\frac 1 2 k_1 x^2 = \frac 1 2 k_2 y^2$ holds if S1 is at its natural length when block B is at its leftmost position and block M1 is not moving. Neither is credible.

We don't know the ratio of the mass of block B wrt blocks M1 and M2, so I am inclined to claim the exercise as stated in post #1 isn't just complicated: it's unsolvable



$\$

 

[PeroK]

I have a nagging feeling, nevertheless. Block B is released and S1 starts to decompress, transferring spring energy that is converted to kinetic energy of block B plus spring energy from the compression of S2 plus kinetic energy of block M2.

At the moment when block B is passing its original position ('$y=0$'), there is also a part of the energy converted to energy to stretch spring S1 (which we know to be at its natural length at that point), plus kinetic energy of M1.

$\frac 1 2 k_1 x^2 = \frac 1 2 k_2 y^2$ holds if S1 is at its natural length when block B is at its leftmost position and block M1 is not moving. Neither is credible.

We don't know the ratio of the mass of block B wrt blocks M1 and M2, so I am inclined to claim the exercise as stated in post #1 isn't just complicated: it's unsolvable



$\$

M1 has "negligible mass".