- #1
Need help quik with this differentiation
- Thread starter houssamxd
- Start date
-
- Tags
- Differentiation
In summary, the conversation discusses a question about finding the derivative using the chain rule and the Fundamental Theorem of Calculus. The question is based on a given function and its integral, and the solution involves using the relevant equations and applying the chain rule.
- #2
tiny-tim
Science Advisor
Homework Helper
- 25,839
- 258
hi houssamxd! 
(is the question to find dy/dx?)
why can't you just use the first of your "relevant equations"?
(is the question to find dy/dx?
)why can't you just use the first of your "relevant equations"?
- #3
Mark44
Mentor
- 37,784
- 10,175
$$\text{Let}~ G(x) = \int_0^x (t^3 + 1)^{10}dt$$houssamxd said:Homework Statement
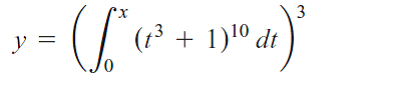
Homework Equations
[itex]\frac{d}{dx}[/itex]
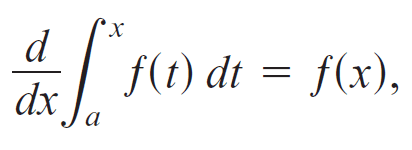
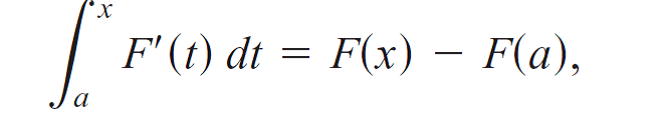
The Attempt at a Solution
i couldn't do it because we didnt learn this type of question
Then y = [G(x)]3
How would you find dy/dx?
- #4
HallsofIvy
Science Advisor
Homework Helper
- 42,988
- 981
So your question is to find the derivative [itex]d u^3/dx[/itex] where [itex]u= \int_a^x f(t)dt[/itex]?
Surely, you have learned the chain rule:
[tex]\frac{dy}{dx}= \frac{dy}{du}\frac{du}{dx}[/tex]
And to find du/dx, you need the "Fundamental Theorem of Calculus" which you give as a "relevant equation".
Surely, you have learned the chain rule:
[tex]\frac{dy}{dx}= \frac{dy}{du}\frac{du}{dx}[/tex]
And to find du/dx, you need the "Fundamental Theorem of Calculus" which you give as a "relevant equation".
FAQ: Need help quik with this differentiation
What is the purpose of differentiation in science?
Differentiation is the process of determining the rate of change of a function or variable. In science, it is used to analyze how one variable changes in response to another, and is essential in understanding complex systems and relationships.
How do you perform differentiation?
To differentiate a function, you need to use the rules of differentiation which include the power rule, product rule, quotient rule, and chain rule. These rules involve finding the derivative of each term in the function and then combining them to find the overall derivative.
What is the difference between differentiation and integration?
Differentiation and integration are inverse operations of each other. While differentiation finds the rate of change of a function, integration finds the total change over a given interval. They are often used together to solve problems in calculus.
When is differentiation used in real life?
Differentiation is used in many real-life situations, including in economics to analyze supply and demand, in physics to understand motion and forces, and in biology to study growth and decay.
Can you give an example of differentiation in action?
One example of differentiation in action is in the field of medicine. Doctors use differentiation to analyze the rate of change of a patient's symptoms to determine the best course of treatment. They can also use differentiation to monitor the effectiveness of a treatment over time.