Need help to verify an attempt to explain strain as point property

[scoutfai]

Recently I review some old text and browse around the internet to read about definition of strain and stress. I come across the following document

http://web.mit.edu/emech/dontindex-build/full-text/emechbk_4.pdf

Previously I have been facing difficulty trying to come out with an explanation of what it means by strain as a point property in a solid continuum. I knew there is formal explanation and definition out there, but they are hard to visualize (to me at least). This MIT document has inspire me to think of something and I wish to get some verification on the thought, whether it is valid or not, if not, why.

The objective is to explain what it means by strain in a general solid continuum, where the shape is not simple geometry, no well define length width and height, hence one just can not get an original length to divide the elongation when the object is under load. Beyond that, is to try to show that, at different point in a solid continuum, there can be a strain exists there, though it might be constant throughout the solid in simple case.

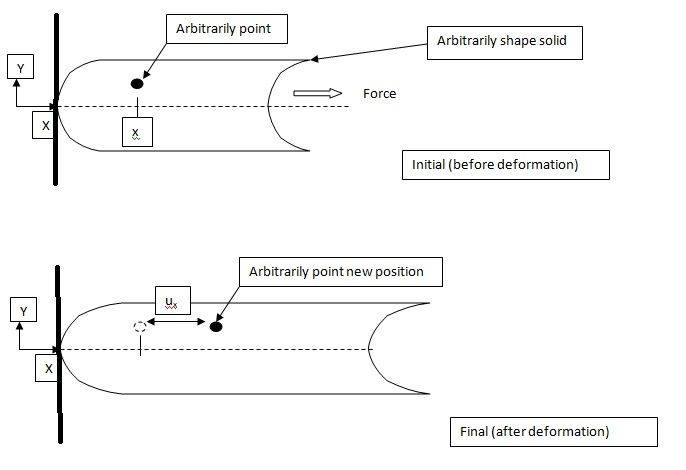
Imagine a load case as illustrate above in the picture. The arbitrarily solid is being fix at the thick black line. An arbitrarily force is applied at the other end. It can be any direction, but for simplicity I only take the x-direction. Now we can choose any point in the solid, which has x-coordinate x.

The displacement of this point due to load along x-direction is indicated as $u_{x}$.

Then the strain of this point along x-direction, $\epsilon_{x}$ is equals to

$\epsilon_{x}$ = $\frac{du_{x}}{dx}$

i.e. strain is the rate of change of point displacement with respect to position.

In this way one can see every point (different x) will have a strain. There is no need to bother about the original length (we cannot find it any way, is an arbitrarily shape solid).

Remark: you can immediately see that this is just a copy and paste of the demonstration in the MIT document at section 4.6.

Any mistake here?

I remember true strain being defined as
$d\epsilon=\frac{dl}{l}$ , where l is the length of object. It looks different than my equation. So I think maybe I made mistake?

Lousy drawing using Microsoft Word, please bear with me on that.

 

[Chestermiller]

The easiest way to understand strain in a deformed solid is to use "material coordinates." Let x(X) be the position of a material particle after deformation that was at position X before deformation. The position before deformation serves as a label for the particle, and is referred to as its material coordinate. If, before deformation, there were two neighboring material particles that were at locations X and X + dX, after deformation, these same two neighboring material particles will be located at x and x + dx. The local strain on the material element between x and x + dx is given by dx/dX -1 (final length divided by original length minus 1). But dx/dX -1 = d(x-X)/dX. And x - X is the displacement u_x. So,

Local Strain = du_x/dX. If the strain is very small, then the dX in the denominator is virtually equal to dx. So,

Local Strain = du_x/dx

 

[scoutfai]

The easiest way to understand strain in a deformed solid is to use "material coordinates." Let x(X) be the position of a material particle after deformation that was at position X before deformation. The position before deformation serves as a label for the particle, and is referred to as its material coordinate. If, before deformation, there were two neighboring material particles that were at locations X and X + dX, after deformation, these same two neighboring material particles will be located at x and x + dx. The local strain on the material element between x and x + dx is given by dx/dX -1 (final length divided by original length minus 1). But dx/dX -1 = d(x-X)/dX. And x - X is the displacement u_x. So,

Local Strain = du_x/dX. If the strain is very small, then the dX in the denominator is virtually equal to dx. So,

Local Strain = du_x/dx

Thanks for the enlightenment. Your explanation is way more general than mine. I see your equation and mine equation almost the same form. Can I say I am not wrong? But can I say I am right about my equation and reasoning?

 

[Chestermiller]

Thanks for the enlightenment. Your explanation is way more general than mine. I see your equation and mine equation almost the same form. Can I say I am not wrong? But can I say I am right about my equation and reasoning?

Yes, you can say you are not wrong, and that you are right in your equation and reasoning. I just wanted to present you with a more structured way of starting to think about it that carries over into more general developments where the deformation is not 1D, and the strains are large. I also wanted to show why local strain determined in this way for non-homogeneous deformations is consistent with your experience with the global strain for homogeneous deformations.

Chet