al4n
- 17
- 0
We have 2 objects, m1 and m[SUPlB]2[/SUB]
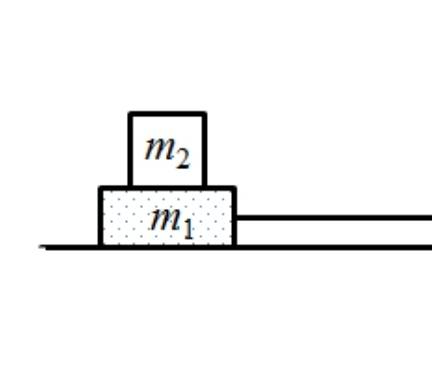
Friction is present between the two objects but not between m1 and the floor. A force is exerted on the bottom object which causes it to accelerate parallel to the floor. The thing I'm wondering for while now is, how do I prove that the acceleration of the top object is equal to the acceleration of the bottom object when the magnitude of the applied force is within some range?
Friction is present between the two objects but not between m1 and the floor. A force is exerted on the bottom object which causes it to accelerate parallel to the floor. The thing I'm wondering for while now is, how do I prove that the acceleration of the top object is equal to the acceleration of the bottom object when the magnitude of the applied force is within some range?