megapiano
- 7
- 0
- TL;DR Summary
- I need help modifying my N-body simulation's force calculation formula so that galaxy simulations give rise to a spiral-arm aesthetic.
Many years ago, for my high school senior project, I wrote a solver for the N-body problem that is performance-optimized using the Barnes-Hut algorithm. (the optimization algorithm is not relevant to my question.)
In one particular simulation, I simulated a spiral galaxy. The simulation is not meant to be scientifically accurate, but is instead meant to demonstrate the simulator. You can view a video of this simulation below:
Now, as you can see in the video, the galaxy develops pseudo-spiral-arms. I say "pseudo" because the arms are not developed according to density wave theory. Instead, I incorporated a trigonometric function, such as
Here are a couple screenshots from the video that show that
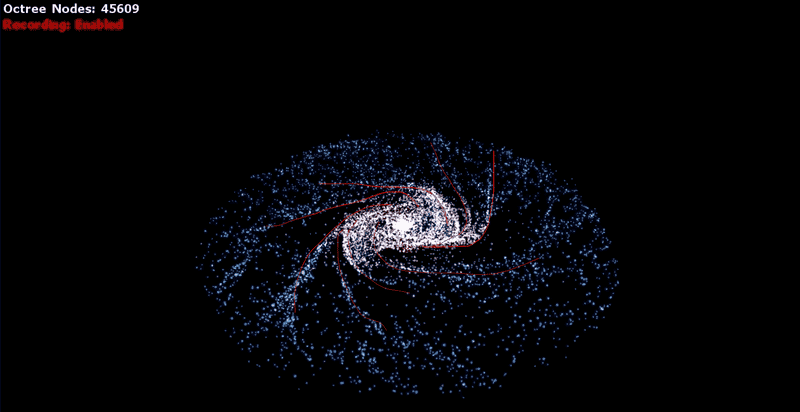

The problem: Now, many years later, I have recovered the source-code of the simulator that is an earlier version of what is used in the video. And in the force calculation of this version of the code, there is no
After many attempts I am unable or recreate the argument that I passed to the
Here is the force calculation as derived from Newton's law of gravitation. The smoothing variable is used to prevent singularities from forming and also to prevent wild sling-shot effects:
forceGravity is a quantity and I calculate the 3d vector to apply to both of the particle's acceleration vectors according to their relative positions.
So, somewhere in there was a
Can anyone figure out/know how to re-implement
Any help is greatly appreciated.
In one particular simulation, I simulated a spiral galaxy. The simulation is not meant to be scientifically accurate, but is instead meant to demonstrate the simulator. You can view a video of this simulation below:
Now, as you can see in the video, the galaxy develops pseudo-spiral-arms. I say "pseudo" because the arms are not developed according to density wave theory. Instead, I incorporated a trigonometric function, such as
sin(), in the gravity-force calculation of the particles. Without this addition, "vanilla" N-body simulations of galaxies do not develop the spiral arm structure you see in the video.Here are a couple screenshots from the video that show that
sin() is being used in the force calculation as evidenced by the wave-like streams of particles annotated by the red lines (note that there are N >2 arms in these screenshots. In the video, if you keep watching, the number of these is reduced and the existing arms grow in size.)The problem: Now, many years later, I have recovered the source-code of the simulator that is an earlier version of what is used in the video. And in the force calculation of this version of the code, there is no
sin() implementation in the force calculation, and thus, I cannot reproduce the spiral-galaxy aesthetic that is seen in the video: the pseudo-spiral-arms do not form.After many attempts I am unable or recreate the argument that I passed to the
sin() function or where I even put it in the force calculation.Here is the force calculation as derived from Newton's law of gravitation. The smoothing variable is used to prevent singularities from forming and also to prevent wild sling-shot effects:
forceGravity = (G * particleMass1 * particleMass2) / (distanceBetweenParticles^2 + smoothing)forceGravity is a quantity and I calculate the 3d vector to apply to both of the particle's acceleration vectors according to their relative positions.
So, somewhere in there was a
sin() function that gave rise to the aesthetic of spiral arms.Can anyone figure out/know how to re-implement
sin() in the force calculation? I think it was used as a coefficient or something, but I'm unsure what I passed as the parameter to the function. Candidates for variables used in the formula passed as the parameter may include: distance to galactic center, expected galactic radius, something to do with the position of the particles relative to the galactic center, or others that I can't think of.Any help is greatly appreciated.