Neutron scattering probability distribution

[evceteri]

Hi, I'm reading Chapter 2-II of of Duderstadt & Hamilton's "Nuclear Reactor analysis". In the section "Differential scattering cross sections with upscattering" it is discussed the situation in which neutrons suffers elastic scattering collisions in a hydrogen gas at finite temperature T and the nuclei are in motion with a Maxwell - Boltzmann velocity distribution.

For this case they cite the scattering probability as given by

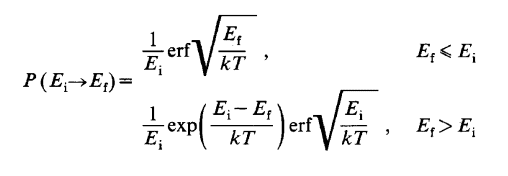
where

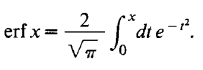
Then they plot the probability distribution for some incident neutron energies:

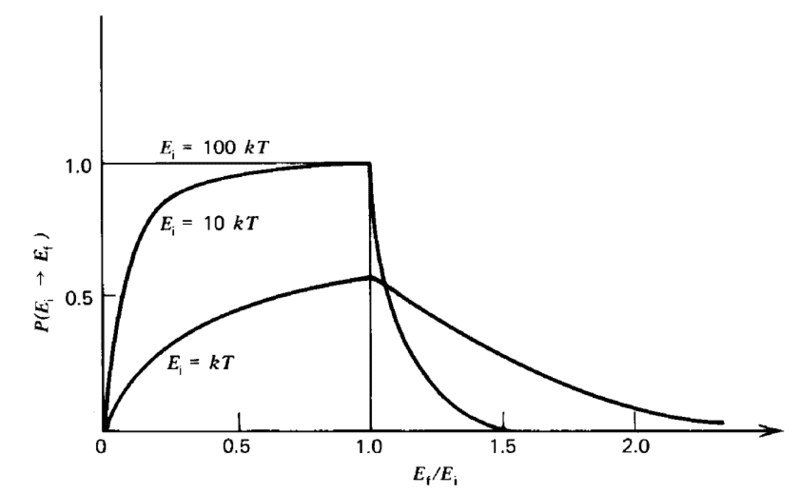
I've been trying to reproduce this plot but I just don't seem to understand how.

So, for example, if $E_i = kT$ and $E_f/E_i = 1.0$ then $E_f = kT$ and $$P(E_i \rightarrow E_f) = \frac {1} { kT} erf \sqrt { \frac {kT} {kT}} = \frac {0.84} {kT}$$.

I'm not sure what I'm supposed to do next, as the expected result in the plot is about 0.5. I know $P(E_i \rightarrow E_f)$ is a probability distribution so in order to get rid of the $kT$ I need to integrate but from where to where?

Can you help me figure it out?

 

[Charles Link]

I don't think it is exact, in that to the best I can tell, the probability function isn't precisely normalized to unity. Perhaps someone else can weigh in and confirm my preliminary assessment here.
$\int\limits_{x_o}^{+\infty} e^{-t^2} \, dt \neq e^{-x_o^2}$, and it looks like they might have thought that it is. There is also a factor of $2/\sqrt{\pi}$, but it still won't normalize properly.
$\int\limits_{x_o}^{+\infty} e^{-t^2} \, dt=\int\limits_{0}^{+\infty} e^{-(t+x_o)^2} \, dt=e^{-x_o^2} \int\limits_{0}^{+\infty} e^{-(t^2+2 x_o t)} \, dt$. Perhaps they overlooked the $2 x_o t$. If the $2 x_o t$ weren't there, I think it might normalize how they wanted it to.

 

[Astronuc]

I don't think it is exact, in that to the best I can tell, the probability function isn't precisely normalized to unity. Perhaps someone else can weigh in and confirm my preliminary assessment here.

I had a similar thought. I was wondering if the equations are correct in DH. They are also found in John Lamarsh's Nuclear Reactor Theory. We had to derive the equations. As far as I remember, the plots are correct. When E_i >> kT, i.e., the neutrons have much greater energy than the hydrogenous material, there is no upscatter. Upscattering occurs as the neutron energy approaches thermal equilibrium with the hydrogen.

The value 0.84 is about a factor of 1/ln2 * 0.58, which is about the value where E_i = kT.

I'd have to find my copies of Lamarsh and DH to compare the developments of the equations.

 

[Charles Link]

@PeroK Might you take a look at the above formulas and see if you concur with my assessment. Thanks. :)

 

[rpp]

Similar equations and a figure with a little more resolution are given in Lamarsh, "Nuclear Reactor Theory", on page 243. In the Lamarsh figure, the intercept looks to be about 0.51.

If you look at the graph for 100*kT, you can see that it makes a box about 1x1, which is the correct normalization for a probability distribution function. Therefore, I am assuming that both the x-axis and y-axis are divided by Ei. The x-axis is marked correctly, but the y-axis is not.

A plot of the results I get is shown below. I added an additional line at 0.5*kT. I can't explain why the intercept in the books is about 0.51 and the intercept we are getting is 0.84 (corresponding to erf(1)).

I looked at the references given by Duderstadt and Hamilton, but they do not have a graph in this form.

 

[rpp]

After a little more investigation, the equations and a similar plot are in Bell and Glasstone, "Nuclear Reactor Theory", 1970. The plot is Figure 7.5 on page 336 and the equations are (7.31) and (7.32) on page 337. The plot in Bell and Glasstone indicates a value close to 0.84 when Ei=Ef=kT.

Bell and Glasstone reference Beckurts and Wirtz "Neutron Physics", 1964. This book has similar equations and a the plot shown below. This plot indicates a value of 0.84 when Ei=Ef=kT.

In conclusion, I believe the figure in Duderstadt and Hamilton is not very precise and the correct intercept should be erf(1). (You have to remember that plots generated in the 60's and early 70's were usually drawn by hand, and may not be as precise as we expect today.)

 

[Charles Link]

I still have no success at showing the probability function is normalized to unity. I can't show or prove it to be incorrect, but I also haven't been able to show or prove that it is normalized to unity.

 

[rpp]

I agree. I tried to integrate it numerically, but it doesn't appear to be normalized to unity.
Here are the approximate sums I calculate with different values of Ei
10kT 1.05
2kT 1.247
1kT 1.471

Now I'm wondering if the equations are missing a normalization factor, and the Duderstadt plot includes a "fixed" normalization factor?

 

[Charles Link]

Very interesting @rpp . Perhaps I was spending a lot of time trying to prove two things equal that simply aren't. Kind of pathetic if multiple textbook authors have propagated the same error, so it would be good to have a definitive answer on this. I had no success proving them to be not equal algebraically,(i.e. the two areas/integrals in question ), but if a numerical integration shows they are far from equal, that is sufficient.