Newbie needs help with angle iron load calculation

[peabody1998]

TL;DR

What dimension aluminum angle can safely carry a 200lb load across a 10ft span?

I am trying to decide on the material and dimensions for the rail. The rails are supported on either side of a 10ft span.

-- What dimension steel angle can carry a 200lb load across a 10ft span? a=? b=? c=?
-- What dimension aluminum angle can carry a 200lb load across a 10ft span? a=? b=? c=?

 

[berkeman]

Welcome to PF.

Is there a reason that you are not planning on bracing those rails underneath? Why try to do this with the rails only supported on the ends?

What happens if this system fails and the roof falls. Could there be people under or near when the roof falls? Do you need to pull any permits for this construction?

 

[peabody1998]

I require the rails to be braced on the ends only. No people under structure. No permits required. I have altered the question to address your concerns. Thank you.

 

[berkeman]

I have altered the question to address your concerns.

Hmm, but one of the alterations was to not show the roof/cart with 2 sets of supporting wheels, which changes the loading on the beam...

 

[Nugatory]

Look at some engineering tables for quantitative data. Even if you don't need to pull a permit, your local jurisdiction's building codes for steel-skin buildings will tell you a lot about what you need to bridge the gap.

How much deflection are you willing to accept? That's likely to drive the design, as beams will deflect past usability under a dynamic load (like rolling the roof on and off) well before there's serious risk of failure.

Ten foot spans will twist under load, a lot. Traditional construction requires some form of side bracing (which we often don't notice because it's provided by some other part of the structure, such as the subfloor) to limit this effect.

Be aware that stiffness across a span depends on the depth of the beam much more than the strength of beam material itself and decreases rapidly as the span increases.

Considering the above, I would be very surprised to find that angle iron is satisfactory, if this were my project I'd already be looking at welding a suitable truss (but I have a welder which makes that an easy path) or using the angle iron as rails on top of appropriately deep 2x lumber or wood truss.

Pay a lot of attention to the connection between rails and roof. Roof supports aren't designed to handle this sort of load without additional bracing underneath, and you do not want a failure here to open up leaks into whatever is underneath the roof.

What winds do you anticipate? Where I live 50+mph thunderstorms are an annual thing, you may live in a more friendly climate. Again, local building codes will have something about typical wind resistance requirements. You do not want the sliding roof structure being lifted off the rails, or if tied down damaging what it's attached to.

 

[russ_watters]

In isolation the sketch doesn't make a lot of sense to me - the context of what the whole structure looks like probably matters. Roll off-roof observatories are a pretty common thing - have you looked at similar designs for ideas? Such as:
https://www.astrogfk.com/roll-off/

This one looks an awful lot like what @Nugatory described: a rail on top of a 2x4.

 

[Nugatory]

This one looks an awful lot like what @Nugatory described: a rail on top of a 2x4.

It does indeed... Although 200 lbs and a ten-foot span is going to want more than a 2x4, that's the general concept. Beam span tables in the building code are where the truth will be found.

 

[Baluncore]

Should it be "angle iron", or "angle aluminium" in the title?

If you can control the axial rotation by attachment to a continuous load, the material will carry more load or have less deflection, if you turn the angle onto its edge, like '<' or '>', rather than '^' or 'V'.

 

[peabody1998]

I have simplified the question further to get a rough idea of what load aluminum vs steel angle can handle.
For example: Given 2"x2"x0.25" angle oriented vertically like '^' supported 10 ft apart with a point weight of 200lbs midway, what is the deflection with aluminum? steel?

 

[Baluncore]

I have simplified the question further to get a rough idea of what load aluminum vs steel angle can handle.

What is the ratio of Young's modulus for iron, to that for aluminium?

My guess is that they are similar, but that aluminium will work harden and fail sooner than steel.

Structurally, you should be using a flexible wire to run a larger diameter pulley, not a solid section that will be stressed where the load travels and hangs on the pulley. You are designing for failure, not safety.

 

[jack action]

I have simplified the question further to get a rough idea of what load aluminum vs steel angle can handle.
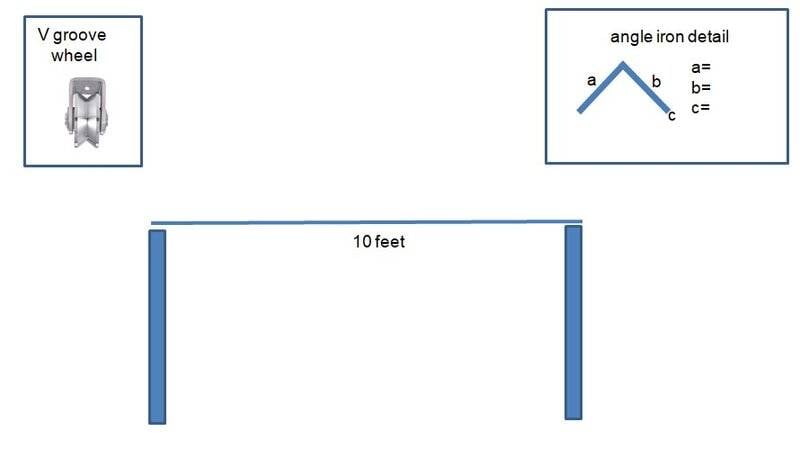
For example: Given 2"x2"x0.25" angle oriented vertically like '^' supported 10 ft apart with a point weight of 200lbs midway, what is the deflection with aluminum? steel?

You haven't simplified the question, you changed it. You asked about "the load that could be safely carried by" and now you are asking about the deflection.

The equations to calculate the maximum deflection for a certain beam under a certain load can be found here - together with a calculator. For the basic case you are asking about:
$$\delta_{max} = \frac{PL^3}{48EI}$$
To calculate the second moment of area $I$, you can find good info - and a calculator - for an angle beam here.

You can find the typical values for Young's modulus $E$ here, i.e. 68 GPa for aluminum and 200 GPa for steel A36.

As for the "safe load" you need to find the maximum stress within your beam. You have the equation here, namely:
$$\sigma = \frac{Mc}{I}$$
We already know $I$ and $c$ is just the longest distance, perpendicularly, from the neutral axis.

For the maximum moment $M$ found on the beam, you can use this calculator and get the maximum value on the moment diagram. For the simple case proposed (a beam of length $L$ with a load $P$ at its center), it is:
$$M_{max} = \frac{PL}{4}$$
For more info on how it is done, find it here (fun stuff!).

The beam will permanently deform once the stress $\sigma$ gets larger than the yield strength of the material. Some typical values can be found here, i.e. 250 MPa for steel A36 and 400 MPa for Aluminum alloy 2014-T6. These numbers can vary widely from different alloys, even different manufacturers.

Then you have to consider the safety factor, which is the yield stress divided by the working stress we calculated. If you are using the equations and approximate numbers I presented here - together with the very simple description of your problem and the obvious lack of knowledge you have about what needs to be done - you probably need a safety factor of at least 10 to be really on the safe side.

And this is why nobody on this forum will give you a straight answer - especially the "safe load" - to this seemingly simple but, oh!, very complex problem.

 

[peabody1998]

Thank you! I greatly appreciate the information.