Newton's 3rd Law interactions with 2nd and 1st Law Partners

[skybee]

TL;DR Summary

Where do partner forces come into play?

I was over on the stack but got asked to move over here.
https://physics.stackexchange.com/questions/804903/newtons-3rd-law-force-on-a-rocket

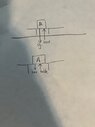
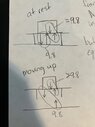
I've been at it all day trying to understand what partner forces are and how you can have a change in force with regard to them, or why gravity is special and not a partner force to the upward force on this table. Suppose you have a table sitting on the ground with a box on top. I've been told the partner force is between box A and table B (an equal and opposite force), but there is also a partner force between A and the ground g. And somehow at the same time there's only gravity pulling this box down and the table pushing it up. At some point force increases to push the table upward, I would like to know how that affects the rest of the forces. It really does not make sense. I've been trying different variations of free body diagrams to see if something clicks but no matter what I put it seems like something is contradicting something else.

 

[Orodruin]

The third law partners never act on the same object. This is the thing to remember. The third law states that if object A acts on object B with a force $\vec F$, then B acts on A with a force $-\vec F$.

In the case of gravity from the Earth on the box, the third law partner is the force of gravity from the box on the Earth. When you are considering equilibrium for the box, the force from gravity on the box and the force from the table on the box are equal in magnitude and opposite in direction, but they are not a third law pair. They cannot be because they act on the same object. The reason they are equal in magnitude and opposite in direction is that they are the only forces on the box and the box is assumed to be in equilibrium. As such it is a result from the second law and the equilibrium assumption. If the box was not in equilibrium, these forces would not necessarily be the same - such as when the box stops when you drop it on the table - nor do they need to be the same if there are additional forces acting on the box - such as you attempting to lift the box.

 

[Orodruin]

Also note that your drawings are not free body diagrams. A free body diagram draws a single object and the forces acting upon it.

 

[skybee]

I get that they aren't a pair. The pair is between the box/ground and then the box/table. I think I'm starting to understand, but originally I had previously taken "only forces" to mean only half of a pair. That's why I was so confused about that because that wouldn't make sense. Now I understand that to mean these pairs are the only forces on the box. I've been browsing and saw one of your old posts talking about adding force to the box like putting a hand on it and the forces changing. My understanding now is that if there is force applied to the box or if the table were to accelerate upward like in my example, that the weight of the box would not change but the force between the box and table would.

So I think I get it now. The weight of the box is not partnered with the upward force of the table, but at rest it happens to equal the partnered force of the box on the table.

Single object = free body diagram. Gotcha.

Please let me know if I'm still getting it wrong or if it's finally correct.

 

[Orodruin]

I've been browsing and saw one of your old posts

There are a couple to choose from …

talking about adding force to the box like putting a hand on it and the forces changing.

I am nothing if not consistent… although apparently I change direction of the extra force from time to time. Pushing the box down is an easier example though as you don’t have to limit the magnitude. I must be getting dumber…

 

[skybee]

There are a couple to choose from …


I am nothing if not consistent… although apparently I change direction of the extra force from time to time. Pushing the box down is an easier example though as you don’t have to limit the magnitude. I must be getting dumber…

Thanks for your help!

 

[cianfa72]

Just to add to what @Orodruin said in post #2: the analysis about the forces acting on the box as done (in particular the use of Newton 2nd law on it) makes sense only with respect to an inertial frame. In that case we can conclude that the two forces acting on the box are actually equal in magnitude and opposite.

 

[Chestermiller]

Here are the action/reaction pairs:

1. (Downward) force box exerts on table and (Upward) force table exerts on box.
2. (Downward) force table exerts on floor and (Upward) force floor exerts on table.
3. (Downward ) body force earth exerts on box and (Upward) body force box exerts on earth.

Contact action/reaction pairs are easy to spot since they happen at the same contact surface (e.g. 1 and 2). Body action/reaction pairs are more difficult to spot because they occur at a spatial distance (e.g., 3)

 

[Orodruin]

Body action/reaction pairs are more difficult to spot because they occur at a spatial distance (e.g., 3)

Here it helps having a fully relativistic field theory at hand - such as Maxwell’s electromagnetism. There simply are no actions at a distance and everything is local. You can do similar things in gravity as well but it is somewhat less nice due to the infinite propagation speed in Newtonian gravity (and the relativistic theory doesn’t have gravity as a force really).