Newton's second law (My turtle named Newton being accelerated)

[rgtr]

Homework Statement

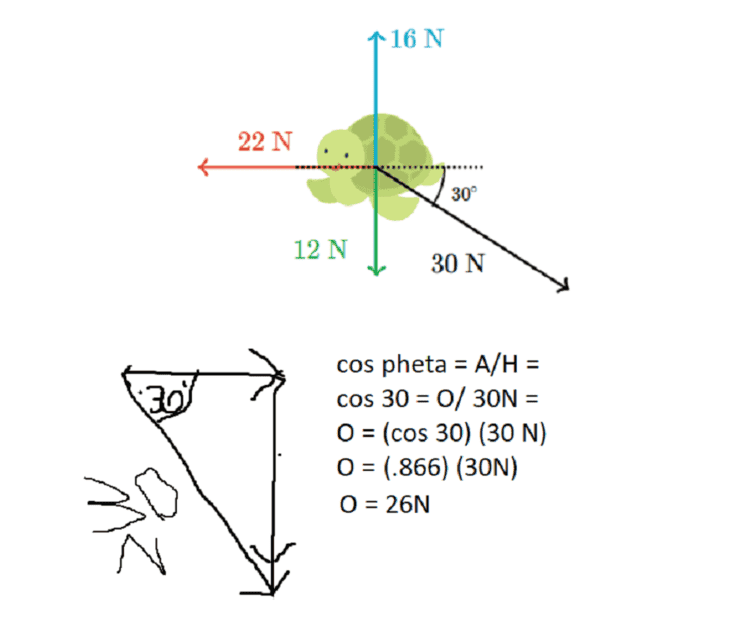
A 1.2 kg turtle named Newton has four forces exerted on it as shown in the diagram below.
What is the horizontal acceleration of Newton the turtle?
What is the vertical acceleration of Newton the turtle?

Relevant Equations

$f = ma$

https://www.khanacademy.org/science...s-laws-of-motion/a/what-is-Newtons-second-law

How do I find the horizontal right components force? It states it is 22 N but there is no reason that the left horizontal component is the same as the right. I thought the horizontal right components force is 26N? Where did I go wrong?

Here is my attempt.

If my picture isn't clear I can use latex to make it look nicer just let me know.

 

[DaveE]

Read that web page again, more carefully. They agree with you: 26N to the right minus 22N to the left. The net horizontal force is 4N to the right.

 

[rgtr]

Also I typed O when it should be A.

 

[rgtr]

C^2 - B^2 = A^2
A^2 is the opposite of the triangle.
30^2-26^2=
900N-676N= 638N
square root A^2 gives me A.

The answer is 15N.
But the x top component is 16N and the bottom x component is 12N. I always thought A^2 should be 16N or 12N?
Thanks for the help.
Is okay if I didn't type this in latex? If you want me to let me know.

 

[DaveE]

I think you've misunderstood the problem and thus the diagram. Reread it carefully.
"A 1.2 kg turtle named Newton has four forces exerted on it as shown in the diagram below."
There are 4 forces applied to the turtle, that is what the 4 vectors are in the diagram.
Since they are asking for the acceleration in the vertical and horizontal directions, you need to find the net force in each of those directions. Fortunately 3 of the 4 forces are already aligned, but the black 30N force isn't.

So the heart of the problem is to express the 30N force as the sum of two forces, each of which is aligned with either the vertical or horizontal axis. You'll use simple trigonometry to do this. Then you will be left with 5 force vectors each of which is aligned horizontally or vertically. The rest of the solution is to simply add up the forces on each axis to get a net horizontal force and a net vertical force. These will give you the two accelerations using F=ma.

 

[rgtr]

I don't think I explained the question properly the first time. Let me try to explain it this time. I edited my post it shouldn't have too much of an effect on my question. I have to add the vertical component of the triangles below called A^2. Why doesn't A^2 affect the turtles vertical force component. For example what to find the vertical component force I go 16N- 14N = 4N. But why don't I go 16N - 14N - A^2?

 

[DaveE]

Slow down. Read that web page carefully, they have described the solution. You already used A for the horizontal component of the 30N force. So now, I guess you're reusing that variable as the vertical component? Also why A^2? I can't find any 14N force in this problem either. I suspect you're just being sloppy. Your basic trig concepts seem correct, but I think you're confused about describing and adding up the force vectors.

Read what I described earlier about turning the 4 force vectors into 5 which are aligned vertically and horizontally. Draw the 2 new force vector you created on the diagram. Then add up all of the horizontal forces and then the vertical ones.

BTW: I think what you're calling A^2 now, I would call
$30N⋅sin(30^o)$, or $\sqrt{30N^2 - (30N⋅cos(30^o))^2} = 30N\sqrt{1-cos(30^o)^2}$.

 

[PhDeezNutz]

In response to post # 4.

I think you misunderstand the question and you are making it more difficult it than it is.

It is not saying the the 16 N force up and 12 N force down is a result of the angled force. But rather those forces are present along with the angled force.

That’s my 2 cents. I hope I’ve deciphered your posts correctly.Soon you will encounter problems where “the block (turtle) is vertically stationary on the table and an angled force is applied….what is the normal force?”

I think you are confusing the two types of problems. There will be plenty of time for the second type of problem.

 

[Steve4Physics]

Hi @rgtr. I will chip in too.

The 30N force can be split (resolved) into 2 components:
x component = 30cos(30º) = 26N (approx.)
y component = 30sin(30º) = -15N (negative as you can see from the diagram it is in the -y direction)

This means the 30N force can now be totally replaced by these 2 components.

In the x direction, we now have 22N to the left and 26N to the right.
Net force in x direction = -22N + 26N = 4N

In the y direction, we now have 16N up, 12N down and 15N down.
Net force in y direction = 16N - 12N - 15N -= -11N

No ‘squaring’ or ‘square rooting’ is used in this particular problem.

 

[rgtr]

Slow down. Read that web page carefully, they have described the solution. You already used A for the horizontal component of the 30N force. So now, I guess you're reusing that variable as the vertical component? Also why A^2? I can't find any 14N force in this problem either. I suspect you're just being sloppy. Your basic trig concepts seem correct, but I think you're confused about describing and adding up the force vectors.

Read what I described earlier about turning the 4 force vectors into 5 which are aligned vertically and horizontally. Draw the 2 new force vector you created on the diagram. Then add up all of the horizontal forces and then the vertical ones.

BTW: I think what you're calling A^2 now, I would call
$30N⋅sin(30^o)$, or $\sqrt{30N^2 - (30N⋅cos(30^o))^2} = 30N\sqrt{1-cos(30^o)^2}$.

Sorry I must have been tired or multitasking or just wasn't paying close attention.
Also for the A variable one more question how do I know if the vector is pointing up or down?