- #1
LloydGarmadon
- 2
- 0
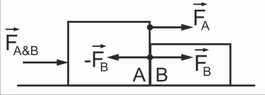
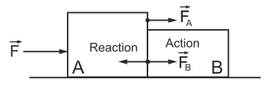
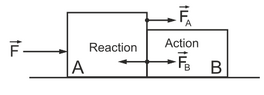
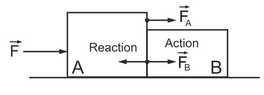
Newton's Third Law states that forces occur in pairs of equal magnitude acting in opposite directions on opposing bodies. When we push against a wall, the wall pushes back with a force of equal magnitude and we move as a result of not being inert enough. What would the force pair be if an astronaut pushes against nothingness in space? Is the reaction pair within the body, and the fist accelerates orders of magnitude more noticeable than the body due to difference in inertia?