- #1
DoobleD
- 259
- 20
In classical mechanics, angular momentum, L = r x p, depends of r. For a given momentum p, the bigger r is, the bigger is the angular momentum. Event in spherical coordinates, r still appears in the classical angular momentum.
However, the angular momentum operator in QM has no r dependence, it's only a function of angles phi and theta. While I can follow the derivation of the operator, I find it surprising that the r dependency vanishes. How can we explain this physically ?
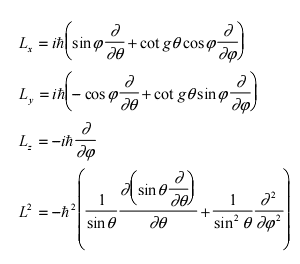
However, the angular momentum operator in QM has no r dependence, it's only a function of angles phi and theta. While I can follow the derivation of the operator, I find it surprising that the r dependency vanishes. How can we explain this physically ?