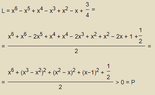No Real Zeroes of $x^6-x^5+x^4-x^3+x^2-x+\dfrac{3}{4}$

  • MHB
  • Thread starter anemone
  • Start date
  • #1

anemone

Gold Member
MHB
POTW Director
3,884
11,585
Prove that the polynomial $x^6-x^5+x^4-x^3+x^2-x+\dfrac{3}{4}$ has no real zeroes.
 
  • #2
:
 

Attachments

  • 12.PNG
    12.PNG
    2.3 KB · Views: 45

Suggested for: No Real Zeroes of $x^6-x^5+x^4-x^3+x^2-x+\dfrac{3}{4}$

MHB Solve Equation: $x^4+2x^3-x^2-6x-3=0$
Replies
7
Views
678
MHB Solve $x^4+(4-x)^4=32$ Equation
Replies
2
Views
502
MHB -s6.6 solve exponential eq 3^x-14\cdot 3^{-x}=5
Replies
1
Views
483
MHB Equation 2: Prove that ##x^2+2x\sqrt x+3x+2\sqrt x+1=0##
Replies
4
Views
565
A Why the triangle inequality is greater than the 2 max{f(x),g(x)}
Replies
1
Views
316
MHB 6.1.5 Solve 5^x+2=12
Replies
4
Views
667
MHB Factorize 6(x^5+y^5+z^5)-5(x^2+y^2+z^2)(x^3+y^3+z^3)
Replies
1
Views
622
MHB Solving $x^3+y^3=7$ and $x^2+y^2+x+y+xy=4$ System of Equations
Replies
1
Views
535
MHB -6.1.12 solve for x 3^{2x}=105
Replies
6
Views
668
MHB Solve $2+5\ln{x}=21$: Find $x$
Replies
5
Views
616

Hot Threads

Recent Insights

Back
Top