MHB Noelia's question at Yahoo Answers regarding use of a Venn diagram

[MarkFL]

Here is the question:

Please help you must draw Venn diagrams and solve with equation, but I can't seem to get the answers!

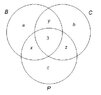
There is a seminar in which 34 students participated. Every student got a certificate, 14 in biology, 13 in chemistry and 21 in physics, and only 3 students got all three certificates. How many got certificates in only one area and how got certificates in only two areas?? Please help you must draw Venn diagrams and solve with equation but i can't seem to get the answers

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Noelia,

First, let's draw the Venn diagram:

View attachment 1144

The set $B$ represents those students who got a certificate in biology, $C$ represents those students who got a certificate in chemistry, and $P$ represents those students who got a certificate in physics.

We are told the cardinality of set $B$ is 14, so we may write:

$$a+x+y+3=14\implies a=11-(x+y)$$

We are told the cardinality of set $C$ is 13, so we may write:

$$b+y+z+3=13\implies b=10-(y+z))$$

We are told the cardinality of set $P$ is 21, we we may write:

$$c+x+z+3=21\implies c=18-(x+z))$$

Hence, the number of students that received only 1 certificate is:

$$a+b+c=39-2(x+y+z)$$

The number of students that received 2 certificates is:

$$x+y+z$$

And we are told the the number of students that received 3 certificates is:

$$3$$

The sum of these is 34, since we are told every student received at least one certificate:

$$39-2(x+y+z)+x+y+z+3=34$$

$$x+y+z=8$$

And so:

$$a+b+c=39-2(8)=23$$

And so we may conclude that 3 students received 3 certificates, 8 students received 2 certificates, and 23 received 1 certificate.