- #1
TimeRip496
- 254
- 5
I don't understand how the author get to these point. Please help me as i have been spending so much time trying to figure this out but to no avail. Thanks for your help
Source: http://phys.columbia.edu/~nicolis/NewFiles/Noether_theorem.pdf
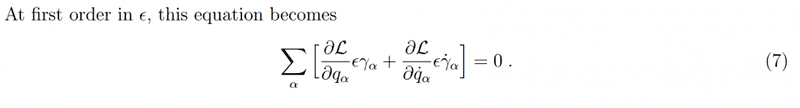
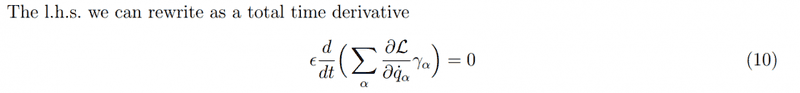
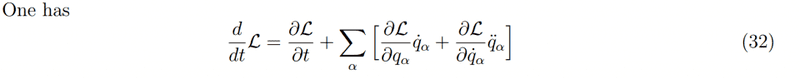
Source: http://phys.columbia.edu/~nicolis/NewFiles/Noether_theorem.pdf