- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading P.M. Cohn's book: Introduction to Ring Theory (Springer Undergraduate Mathematics Series) ... ...
I am currently focused on Section 2.2: Chain Conditions ... which deals with Artinian and Noetherian rings and modules ... ...
I need help with understanding an aspect of the proof of Theorem 2.2 ... ...Theorem 2.2 and its proof (including some preliminary relevant definitions) read as follows:

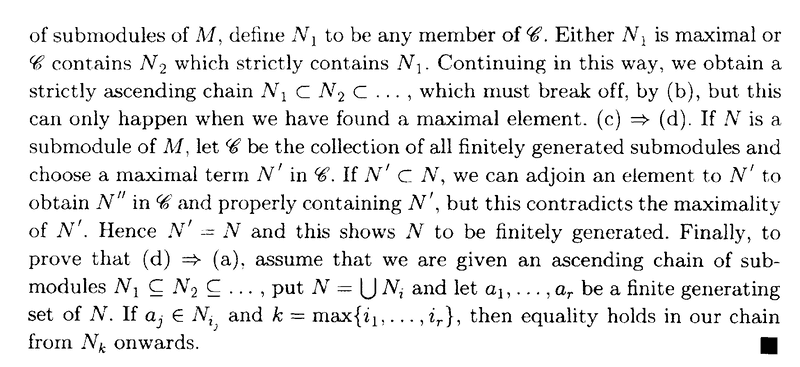
At the end of the above proof by Cohn we read the following:
" ... ... If ##a_j \in N_{i_j} ## and ##k = \text{ max} \{ i_1, \ ... \ ... \ , i_r \}##, then equality holds in our chain from ##N_k## onwards. ... ... "
Can someone please explain how/why ##a_j \in N_{i_j} ## and ##k = \text{ max} \{ i_1, \ ... \ ... \ , i_r \}## implies that equality holds in our chain from ##N_k## onwards. ... ... ?Help will be appreciated ...
Peter
I am currently focused on Section 2.2: Chain Conditions ... which deals with Artinian and Noetherian rings and modules ... ...
I need help with understanding an aspect of the proof of Theorem 2.2 ... ...Theorem 2.2 and its proof (including some preliminary relevant definitions) read as follows:
At the end of the above proof by Cohn we read the following:
" ... ... If ##a_j \in N_{i_j} ## and ##k = \text{ max} \{ i_1, \ ... \ ... \ , i_r \}##, then equality holds in our chain from ##N_k## onwards. ... ... "
Can someone please explain how/why ##a_j \in N_{i_j} ## and ##k = \text{ max} \{ i_1, \ ... \ ... \ , i_r \}## implies that equality holds in our chain from ##N_k## onwards. ... ... ?Help will be appreciated ...
Peter
Attachments
Last edited:
