A Noether's theorem for finite Hamiltonian systems

[thaalves]

TL;DR Summary

How do I write a first integral knowing a symmetry?

The Noether's theorem for finite Hamiltonian systems says that:

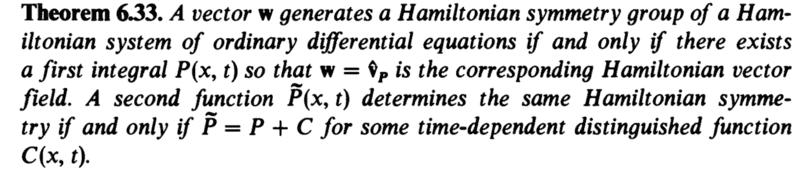
My question is: If I know a symmetry how can I write the first integral?

 

[ergospherical]

If $\mathbf{w}$ is the vector field generating the symmetry then I think you can put $\mathbf{w}(f) = \{ f, P \}$ for an arbitrary function $f$?

 

[thaalves]

In fact my knowledge is very limited in this area, my situation is as follows...
I have the metric, with the metric I can write the Hamiltonian, with the Hamiltonian, can I write the field? if yes, after that do i have to look for a symmetry? Apparently once I have symmetry, Noether's theorem gives me the first integral (his proof in this case), but I'm not getting it.

 

[wrobel]

hope this will not appear to be a severe offtop here

https://www.physicsforums.com/threads/about-the-noether-theorem.996808/