- #1
Jamesan89
- 6
- 0
Hello, thanks in advance for your help,
I am not a physicist, however have a fairly good grasp on mathematics, also this isn't homework or an assignment but a real world problem.
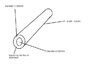
Currently trying to create a system with a nebulising gas at a linear velocity of 350 m/s. The calculations confusing me as the system is complex. The gas flow is through a 100 mm, doughnut shaped tube with an 363 um diameter centre and a 508 um total diameter. The gas flow is currently at 450 ml/min (using a gas flow meter).
My solution would be to convert the flow rate to ml/s (7.5 ml/s) and take the volume of the tube in m^3 by Pi*R^2*h and divide these values, however the output value is clearly not correct. A point in the right direction would be greatly appreciated .
I am not a physicist, however have a fairly good grasp on mathematics, also this isn't homework or an assignment but a real world problem.
Currently trying to create a system with a nebulising gas at a linear velocity of 350 m/s. The calculations confusing me as the system is complex. The gas flow is through a 100 mm, doughnut shaped tube with an 363 um diameter centre and a 508 um total diameter. The gas flow is currently at 450 ml/min (using a gas flow meter).
My solution would be to convert the flow rate to ml/s (7.5 ml/s) and take the volume of the tube in m^3 by Pi*R^2*h and divide these values, however the output value is clearly not correct. A point in the right direction would be greatly appreciated .