Non-linear function with two unknown constants and one variable

[ETBunce]

Am am presented with the problem:

$$
h(t) = c - (d - 4t)^2
$$
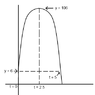
At time t = 0, a ball was thrown upward from an initial height of 6 feet. Until the ball hit the ground, its height, in feet, after $$t$$ seconds was given by the function $$h$$ above, in which $$c$$ and $$d$$ are positive constants. If the ball reached its maximum height of 106 feet at time $$t = 2.5$$, what was the height, in feet, of the ball at time $$t = 1$$?

The answer I am given is 70, but I don't know how to reach that answer. I've tried to solve for the constants but I keep hitting dead ends. I wish I could give more information other than the graph below but that's all I have. Help would be much appreciated, thanks.

I imagine the function if graphed would look something like this:

View attachment 2398

 

[lfdahl]

Hi, there

Thankyou for sharing your problem with us at the MHB.

$h(t) = c -(d-4t)^2$

Try to write down $h(0)$: You know from the initial condition, that $h(0) = 6$ (feet)
Then you should consider mathematically the expression at time $t = 2,5$ where the ball reaches its maximum height (i.e. find the derivative of $h(t)$)

 

[DavidCampen]

Actually, the problem is designed to simplify into solving a system of 2 linear equations in 2 unknowns.

 

[ETBunce]

$h(t) = c -(d-4t)^2$

Try to write down $h(0)$: You know from the initial condition, that $h(0) = 6$ (feet)
Then you should consider mathematically the expression at time $t = 2,5$ where the ball reaches its maximum height (i.e. find the derivative of $h(t)$)

Looks like the ball's height increases by 100 feet over the course of 2.5 seconds. Where do I go from there?

 

[lfdahl]

Looks like the ball's height increases by 100 feet over the course of 2.5 seconds. Where do I go from there?

You still need to find $c$ and $d$, the constants in the expression for $h(t)$.

Therefore, I have asked you to write down the two equations: $h(0) = ...$ and $h'(t=2.5) = 0$

Please give it a try (Wink)

 

[ETBunce]

You still need to find $c$ and $d$, the constants in the expression for $h(t)$.

Therefore, I have asked you to write down the two equations: $h(0) = ...$ and $h'(t=2.5) = 0$

Please give it a try (Wink)

Sorry, I'm confused. Derivatives are used in calculus, right? The problem I am presented with is from a SAT practice test. According to my understanding, I shouldn't need to use calculus tools to solve any of the problems in the SAT.
Should I go learn more about derivatives before trying to solve this problem?
I also have tried working out the equations, and I can't figure out how to solve for $c$ and $d$.

 

[lfdahl]

Sorry, I'm confused. Derivatives are used in calculus, right? The problem I am presented with is from a SAT practice test. According to my understanding, I shouldn't need to use calculus tools to solve any of the problems in the SAT.
Should I go learn more about derivatives before trying to solve this problem?
I also have tried working out the equations, and I can't figure out how to solve for $c$ and $d$.

I´m sorry, I am not familiar with the SAT practice test, but as far as I can see, you do need some knowledge on derivatives of a one-variable function. Anyway, what I was asking you about is the following:

(1). $h(0) = c -(d-4\cdot0)^2 = c-d^2 = 6$

(2). $h'(t) = (-4)\cdot2(d-4t)$ and use $h'(2.5) = 0$ so $d -4\cdot2.5 = 0$

From (2) you can determine $d$. Then you can insert the value for $d$ in (1) and find $c$.

Once you know $c$ and $d$, you can calculate $h(1) = ...$

 

[MarkFL]

If we write the height function in vertex form:

$$h(t)=-16\left(t-\frac{d}{4}\right)^2+c$$

and observe that we are given the vertex $(2.5,106)$

We then immediately have:

$$h(t)=-16\left(t-2.5\right)^2+106$$

And so what is $h(1)$?