Non-uniform Circular Motion & Acceleration

[Cato11]

TL;DR Summary

Non-uniform Circular Motion & Acceleration

I would really appreciate some help with this problem regarding non-uniform circular motion, in which a body is accelerating as it follows a circular path.

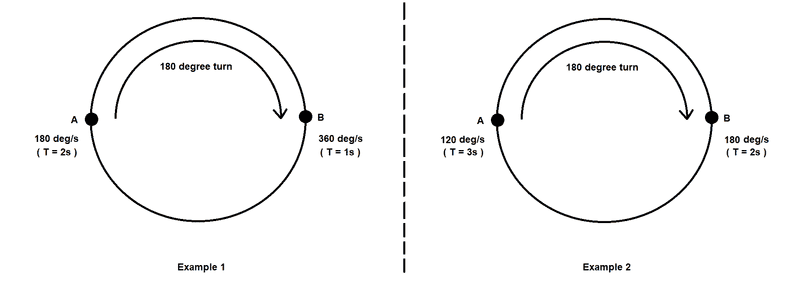
If we take Example 1, a body starts at Point A with an angular speed of 180°/s. The body accelerates to Point B and reaches it some time later with a new speed of 360°/s. Points A and B are exactly 180° apart. What I am trying to understand is:

1. If the body accelerated uniformly from Point A to Point B, how long did the travel time take between the two points?
2. How can we find out what the rate of uniform acceleration is between both points?

If we take Example 2, a body starts at Point A with an angular speed of 120°/s. The body accelerates to Point B and reaches it some time later with a new speed of 180°/s. Points A and B are still exactly 180° apart. The same questions above arise... how does it differ? My instinct tells me the travel time will be longer, with a slower rate of uniform acceleration.

If anyone could help me to answer the two questions I would be enormously grateful. Please comment if further clarification would help.

 

[hutchphd]

There are rotational analogues to all of the equations for linear motion. You need to learn them. They replace linear position with angle (in radians), and mass with moment of inertia. Surely you have seen this?

 

[FactChecker]

Part 1: You have values of T specified in the diagrams that look like time is decreasing. Is that what you wanted? Doesn't the two values of T give the answer to part 1?
Part 2: If you know that the angular rate goes from 180deg/sec to 360 deg/sec in 1 second, what is the angular acceleration (deg/sec per sec)? (Nothing fancy. The answer should be immediate, with no calculations.)

 

[Office_Shredder]

The T= things seem to be indicating how many seconds it takes to do a complete rotation at the given angular speed, and are not intended to denote the current time.

 

[Cato11]

Part 1: You have values of T specified in the diagrams that look like time is decreasing. Is that what you wanted? Doesn't the two values of T give the answer to part 1?
Part 2: If you know that the angular rate goes from 180deg/sec to 360 deg/sec in 1 second, what is the angular acceleration (deg/sec per sec)? (Nothing fancy. The answer should be immediate, with no calculations.)

T is the period of the speed at that point, as Office_Shredder says. It does not denote how long it takes to get from A to B, if it did you are right that it would be an easy calculation.

The challenge is that I know it goes from Point A to Point B, beginning and ending with those speeds. But I do not know how long it takes and what the rate of uniform acceleration is to get there. Does that make sense?

 

[Office_Shredder]

What if instead it said.

The object is moving at 180 meters per second. It accelerates uniformly while traveling in a straight line a total distance of 180 meters. The velocity at the end is 360 meters per second.

What is the acceleration? How long does it take?

 

[Cato11]

Okay so in the case of linear motion, we know that v² = u² + 2as where:

v = final velocity, u = initial velocity, s = distance covered, a = acceleration

So we get a = (v² - u²) / 2s, which in the first example gives a = 270 ms^-2. Solving for the time t,

t = (v - u) / a = 0.66s.

This is a lot simpler though since there is only one component of acceleration. Angular acceleration however has two components right?

 

[Cato11]

My apologies guys, the rotational equivalent is given by an analogous equation as hutchphd said in the first reply. I have solved the problem using those equations. It was a lot simpler than expected.

Again, my apologies for unnecessarily complicating things. Thank you to Office_Shredder for helping me to realize that oversight.

 

[Office_Shredder]

Glad to help. A real thing to keep in mind is these linear formulas are true for motion in any direction, as long as you are describing acceleration in the direction of motion at any point in time. And angular acceleration is acceleration in the direction of motion. You could draw any squiggle you want and describe the velocity along that path and the acceleration in the direction of that path and use the same formula to compute distance traveled.