Non-Uniform Magnetic Field Calculations

[Lachlan]

TL;DR Summary: Need help with figuring out how (or even if I can) to calculate the magnetic field field strength for this non-uniform magnetic field.

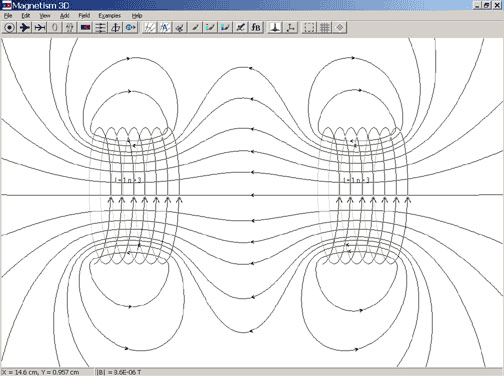I need help calculating the magnetic field strength (if it's possible) in the space between these two solenoids. It is for my year 12 depth study, and I need it to compare it the measured values I obtained experimentally with a magnetic field probe, and visual direction vectors obtained with compasses. If it's not possible to calculate then that's fine, but if it is then whatever you might know can help because I can put that in the report still. I have all the dimensions for the solenoids I used in my experiment and the voltage and current if that helps too.

Any knowledge is helpful, thanks very much.

 

[jambaugh]

I don't have a mathematical theorem in mind but I believe this is a problem with no "closed form solution". This is to say your only going to be able to calculate the field using numerical computations.
I suggest you search "magnetic field software" on your favorite search engine.

 

[Ibix]

The field strength on axis (the straight line across the middle of your diagram) is fairly straightforward and googling "magnetic field on axis of solenoid" will get you good results - equation 12.7.6 here for example. Off-axis, you need elliptic integrals for a single current loop (equations 12-14 in the PDF found here) and then to integrate the result over the two solenoids. It's not impossible to do if you're a confident python programmer (other languages are available, but I know it can be done in python), but it's not simple either.

Does the program you took the screenshot from not give you field strengths? As jambaugh has just commented, it's easier if you can find off-the-shelf software to do it for you.

 

[Lachlan]

The field strength on axis (the straight line across the middle of your diagram) is fairly straightforward and googling "magnetic field on axis of solenoid" will get you good results - equation 12.7.6 here for example. Off-axis, you need elliptic integrals for a single current loop (equations 12-14 in the PDF found here) and then to integrate the result over the two solenoids. It's not impossible to do if you're a confident python programmer (other languages are available, but I know it can be done in python), but it's not simple either.

Does the program you took the screenshot from not give you field strengths? As jambaugh has just commented, it's easier if you can find off-the-shelf software to do it for you.

I found the picture here - http://www.msmedia.com.au/physics/magnetism-3d-sample-screens.html
It seemed to be the only picture that I could find that showed the magnetic flux connection between 2 solenoids, and that's what I'm writing my report on. The program listed is magnetism 3D, and at a cost of $80 isn't something I'd particularly want to spend my money on considering it is just for school, and it requires a windows PC which I don't have. I'd like to able able to do it, but because of time constraints as well I just don't think it's an option. I've looked at a few other program/simulation things, but they all seem to run on windows which doesn't really work for me because I'm also not trying to get windows through bootcamp on my mac.

For the maths, taking one look at it really just blows my mind, I'll take as good as a crack at it as I can so thank you very much for linking it.

Any suggestions for free programs that'll work on mac easy for this in that situation? Also probably helpful mentioning I can't program at all. Yeah I know it seems like I've got quite a few roadblocks here so I completely get it if there's nothing I can do, but whatever suggestions you have help. I have data also from a magnetic field probe of the magnetic field strength along the axis of the solenoid, if that helps.

Thanks for all the help.

 

[Ibix]

If you have some on-axis measurements (or can go back to the lab and get some) the on-axis maths should be manageable for you - you don't need to do the integral, just use the formula after the last equals sign. The off-axis formula is probably out of your reach if you can't program, I'm afraid - numerical integration can be done on paper or supported by Excel and Wolfram Alpha but it requires a fair amount of planning and I wouldn't jump in to the topic with elliptic integrals as a first example.

I don't know anything about magnetic field modelling software I'm afraid. Try googling, including the word "free" or "student" or "education". It isn't uncommon for some pretty good software to be available on 30-day trial or free/cheap for personal/educational use. Also check with your teacher if they can install stuff on school laptops if you can't find it for Mac.

 

[Lachlan]

If you have some on-axis measurements (or can go back to the lab and get some) the on-axis maths should be manageable for you - you don't need to do the integral, just use the formula after the last equals sign. The off-axis formula is probably out of your reach if you can't program, I'm afraid - numerical integration can be done on paper or supported by Excel and Wolfram Alpha but it requires a fair amount of planning and I wouldn't jump in to the topic with elliptic integrals as a first example.

I don't know anything about magnetic field modelling software I'm afraid. Try googling, including the word "free" or "student" or "education". It isn't uncommon for some pretty good software to be available on 30-day trial or free/cheap for personal/educational use. Also check with your teacher if they can install stuff on school laptops if you can't find it for Mac.

The maths for the on axis equation is definitely manageable, could it be assumed that up until the point evenly in between both solenoids (the middle of the straight line across the middle) there is only magnetic flux from the right solenoid involved? And then the reverse for the other half, that it's only the flux from the left solenoid? Or would you need to calculate the flux from both solenoids and then add it together?

 

[Ibix]

You can't neglect the other solenoid's field, no, but yes you can just calculate the field from each solenoid and add them together.

I would use a spreadsheet. Make a column of $x$ values (or whatever you want to call position along the axis), a column of the corresponding $\sin\theta_1$ and $\sin\theta_2$ values for the first solenoid and a column for its field. Then ditto the second pair of $\theta$s and the field. Then a final column adding together the fields. You should be able to enter the formulas once for each column then copy them, so as long as you get the formula right once you reduce the chances of making silly computational errors later.

You can do a lot of sanity checking with that approach. You can plot the $\sin\theta$ values - do they look reasonable? They should all look the same, just shifted along the $x$ axis (assuming your solenoids were identical). Then you can plot the $B$ field from each solenoid - again, should be the same if your solenoids are identical, just shifted along the $x$ axis.

 

[robphy]

You could start here

with a current loop... and do the calculation at points of your choosing.
https://www.glowscript.org/#/user/m...matterandinteractions/program/17-B-loop-xy-xz
which uses the Biot-Savart Law.

Then use superposition of several rings to approximate a solenoid,
then two such solenoids
with the appropriate sizes and locations and currents to model your situation.

You can output the field calculations at points of interest to the console,
formatted in a way to allow easier export to other software.
(For example, I output results from glowscript/webvpython to a comma-separated list
that I can copy-paste into a cell in a desmos script).

Consult the examples at
https://glowscript.org/#/user/GlowScriptDemos/folder/matterandinteractions/
17-Bwire-with-r Magnetic field of a wire
17-B-loop-with-r-dB Magnetic field of a ring, one step at a time
17-B-loop-xy-xz Display magnetic field of a ring, in two planes
17-toroid Magnetic field of a toroid

For interactive visualization purposes,
there are nice visualizations at
https://www.falstad.com/vector3dm/
select "Display: Field Lines"
then
select solenoid
or
select "loop pair stacked" and increase the "Loop Separation"

 

[Lachlan]

You can't neglect the other solenoid's field, no, but yes you can just calculate the field from each solenoid and add them together.

I would use a spreadsheet. Make a column of $x$ values (or whatever you want to call position along the axis), a column of the corresponding $\sin\theta_1$ and $\sin\theta_2$ values for the first solenoid and a column for its field. Then ditto the second pair of $\theta$s and the field. Then a final column adding together the fields. You should be able to enter the formulas once for each column then copy them, so as long as you get the formula right once you reduce the chances of making silly computational errors later.

You can do a lot of sanity checking with that approach. You can plot the $\sin\theta$ values - do they look reasonable? They should all look the same, just shifted along the $x$ axis (assuming your solenoids were identical). Then you can plot the $B$ field from each solenoid - again, should be the same if your solenoids are identical, just shifted along the $x$ axis.

Alright that sounds like a good approach, thank you very much. I'll put that together.

Thanks very much.

 

[Lachlan]

Anyone wants to see how it went, take a look at the finished doc. I changed some stuff so the formatting isn't 100% so it's a word doc so you can edit it where it went wrong. I also put in the excel sheet with all the data in case anyone wants a look.

https://drive.google.com/drive/folders/1mZMGPtdPHOgvrTd4o_5lpMRr9gDOIyAx?usp=sharing