Nonlinear Mass Spring Damper with Euler Bernoulli Beam

[QuantumLollipop]

I'm trying to find a solution to a system in which a clamped free Euler-Bernoulli Beam system rests on top of a mass-spring-damper system. The MSD system has nonlinearities in both the spring and the damper and is of the form:

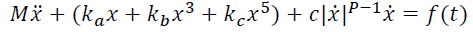
I have extended the nonlinear restoring force to its 3rd term and have enforced the nonlinear damping to obey the power law. I believe this is the correct form for both.

I have no problem solving the Euler-Bernoulli beam problem by itself. That is pretty straight forward. I am mainly interested in an investigation of the modal coordinates, natural frequencies, and behavior of the beam deflection when placed over the MSD system. Obviously the natural frequencies are unaffected since they are a result of material properties. Any thoughts or advice? Thanks in advance.

-QL

 

[Achy47]

Dear QL,

Thank you for sharing your problem and providing detailed information about the system you are working on. From what I understand, you are trying to analyze the behavior of a clamped free Euler-Bernoulli beam system placed on top of a mass-spring-damper (MSD) system with nonlinearities in both the spring and the damper.

Firstly, I would recommend considering the nonlinearities in the MSD system as they will have a significant impact on the overall behavior of the system. Nonlinearities in the spring and damper can lead to complex dynamics and may affect the natural frequencies of the system. It would be helpful to determine the nonlinear stiffness and damping coefficients for the spring and damper, which can be done through experimental testing or analytical methods such as the harmonic balance method.

Next, I would suggest using modal analysis to study the behavior of the beam deflection when placed over the MSD system. Modal analysis is a powerful tool for analyzing the dynamic response of a structure and can provide insight into the modal coordinates and natural frequencies of the system. You can also use modal analysis to determine how the natural frequencies of the beam are affected by the MSD system.

Additionally, it may be beneficial to perform a parametric study by varying the parameters of the MSD system, such as the stiffness and damping coefficients, to see how they affect the modal coordinates and natural frequencies of the beam. This can help you understand how the beam deflection is affected by different configurations of the MSD system.

In summary, I recommend considering the nonlinearities in the MSD system, using modal analysis to study the behavior of the beam deflection, and performing a parametric study to understand the effects of varying the MSD system parameters. I hope this helps and wish you all the best in your research.