Nonlinear optics: electric dipole moment operator

[elemental09]

I am participating in a reading course on nonlinear optics, which is a little difficult since I haven't had any formal education in quantum mechanics other than the standard introductory solving of Schroedinger's eqn. in 1D. Happily this course takes the semiclassical approach, in which the field is classical while all the atomic physics is treated quantum mechanically. The principle text I'm reading from is Nonlinear Optics, 3rd ed., by Boyd.

As an approximate starting point, (in Ch. 3 if you have the text), Boyd derives expressions for the first, second and third order susceptibility tensors. He takes two approaches: first, perturbatively solving the Schroedinger equation, and second, using the density matrix formalism. For both, the system considered is a single atom. In the first approach, it is assumed isolated. The density matrix approach then allows some consideration of the atom's environment. For both approaches he takes a Hamiltonian of the form

http://latex.codecogs.com/gif.latex?\hat{H} = \hat{H_{0}}+\hat{V}(t)
Where

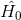is the Hamiltonian of the free atom, and

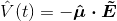
I have two questions to begin with, arising from my lack of background in QM:

1) Boyd refers to the wavefunction under consideration as the "atomic wavefunction". The wavefuntions for the eigenstates of the Hamiltonian then correspond to the quantized energy levels of the atom, but what other meaning is there to the wavefunction? For a single particle, I'm familiar with the probability amplitude for position measurement interpretation of the wavefunction, but this seemingly does not apply to this particular "atomic" wavefunction, as it is not the dynamics of the entire contiguous atom we are interested in, but rather the internal electronic behaviour (polarization and energy). Seemingly, then, we should be considering the wavefunctions of the individual electrons in the atom, though of course I understand that is analytically infeasible. That leads to my next question:

2) What is the meaning of

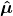? Boyd calls this the electric dipole moment operator. He defines it as

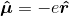, where e is the charge on the electron. However, as discussed above, the states under consideration are atomic states. The individual electrons' wavefunctions are never described. I understand how this operator would be used to characterize the interaction energy of an electron with a classical field, but not an entire, neutral atom. Boyd goes on to compute the expectation value of the atom's electric dipole moment, which is given as:

But this state is that for an atom, not an electron. Intuitively, it seems to me that a calculation of the expectation value of an electric dipole moment should involve the position operator acting on an electron's wavefunction, not an atom's.

I appreciate any effort to help me understand this. Sorry if these are standard textbook questions. If so, please feel free to direct me to a text at a good level (probably late undergrad or early grad QM) that would shed some light on all this.

 

[DrDu]

The absolute square of the atomic wavefunction |\Psi(r_1\ldots r_n) |^2=p(r_1 \ldots r_n) yields the probability density to find an electron in a small volume at r_1, another one at r_2 and so on if there are n electrons in the atom. The (electronic contribution to ) the dipole moment is then -e \int dr_1 \ldots \int dr_n \Psi^*(r_1 \ldots r_n) (r_1+\ldots+r_n) \Psi(r_1\ldots r_n). So basically the atomic wavefunction generalizes the 1 electron case you know to the n-electron case.
PS: Please note that I am too lazy to make explicity that r_1 etc is a three dimensional vector and I also suppressed spin as the dipole moment does not depend on it.

 

[elemental09]

Thanks. That interpretation seems natural. But Boyd writes the atomic wavefunction for an arbitrary atom as being a function of only one spatial variable, and time, which agrees with what you have only for n=1. Similarly, expectation values are calculated as a single integral over all space, not multiple integrals as you have shown. Somehow he is blurring the multi-electron nature of the atom into a one-particle wavefunction.

 

[DrDu]

I don't have the book of Boyd, so I cannot comment on it. However, it is possible to subsume the information relevant for the calculation of one particle properties (and the dipole moment is a sum of the dipole moments of the single electrons, hence it also belongs to that class) in the 1-density matrix.

 

[elemental09]

Sorry it took a while to respond.
In fact before introducing any density matrices, Boyd still treats the atomic wavefunction as one-particle. In any case, I'll have to accept his treatment. But here's another question: the expressions obtained for the susceptibilites using this approach depend on the matrix elements of the electric dipole moment operator with respect to a basis consisting of the eigenstates of the atom. What do these matrix elements represent, and how would one measure them?

 

[Andy Resnick]

I wonder if the missing information is that only one electron participates in the optical process- specifically, the outermost electron.

 

[elemental09]

There could be several valence electrons, though. Though perhaps it is telling that Boyd uses this theory to calculate the third-order susceptibility third-harmonic generation in sodium vapour - sodium having one valence electron.