- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading Hugo D. Junghenn's book: "A Course in Real Analysis" ...
I am currently focused on Chapter 9: "Differentiation on ##\mathbb{R}^n##"
I need some help with the proof of Proposition 9.2.3 ...
Proposition 9.2.3 and the preceding relevant Definition 9.2.2 read as follows:

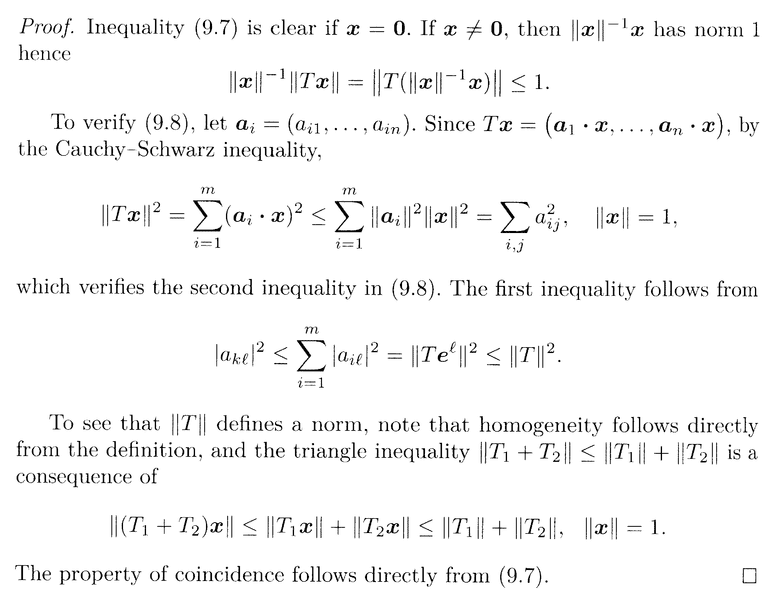
In the above proof we read the following:
" ... ... If ##\mathbf{x} \neq \mathbf{0} \text{ then } \| \mathbf{x} \|^{-1} \mathbf{x}## has a norm ##1##, hence
##\| \mathbf{x} \|^{-1} \| T \mathbf{x} \| = \| T ( \| \mathbf{x} \|^{-1} \mathbf{x} ) \| \le 1## ... ... "
Now I know that ##T( c \mathbf{x} ) = c T( \mathbf{x} )##
... BUT ...
... how do we know that this works "under the norm sign" ...
... that is, how do we know ...##\| \mathbf{x} \|^{-1} \| T \mathbf{x} \| = \| T ( \| \mathbf{x} \|^{-1} \mathbf{x} ) \|##... and further ... how do we know that ...##\| T ( \| \mathbf{x} \|^{-1} \mathbf{x} ) \| \le 1##
Help will be appreciated ...
Peter
I am currently focused on Chapter 9: "Differentiation on ##\mathbb{R}^n##"
I need some help with the proof of Proposition 9.2.3 ...
Proposition 9.2.3 and the preceding relevant Definition 9.2.2 read as follows:
In the above proof we read the following:
" ... ... If ##\mathbf{x} \neq \mathbf{0} \text{ then } \| \mathbf{x} \|^{-1} \mathbf{x}## has a norm ##1##, hence
##\| \mathbf{x} \|^{-1} \| T \mathbf{x} \| = \| T ( \| \mathbf{x} \|^{-1} \mathbf{x} ) \| \le 1## ... ... "
Now I know that ##T( c \mathbf{x} ) = c T( \mathbf{x} )##
... BUT ...
... how do we know that this works "under the norm sign" ...
... that is, how do we know ...##\| \mathbf{x} \|^{-1} \| T \mathbf{x} \| = \| T ( \| \mathbf{x} \|^{-1} \mathbf{x} ) \|##... and further ... how do we know that ...##\| T ( \| \mathbf{x} \|^{-1} \mathbf{x} ) \| \le 1##
Help will be appreciated ...
Peter

