Normal distribution graph P(a<x<b)

[karush]

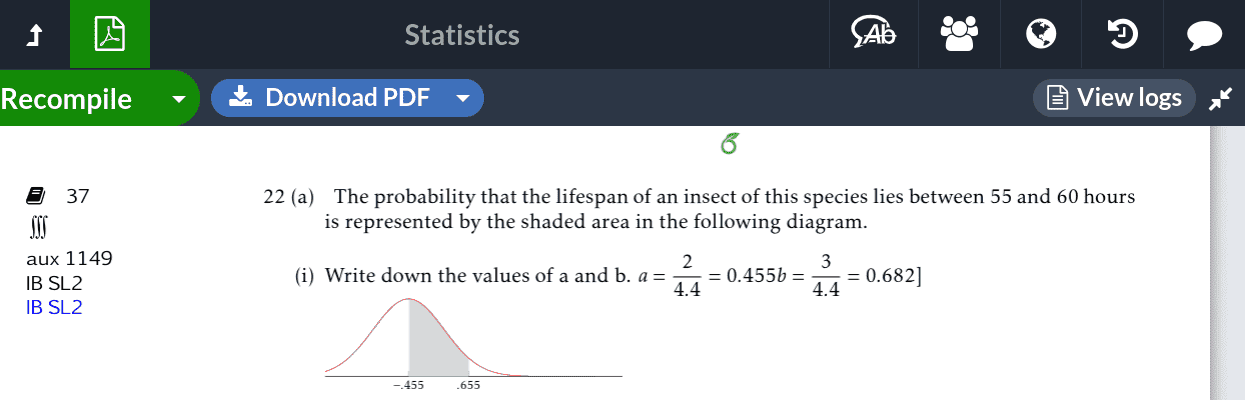
The probability that the lifespan of an insect of this species lies between 55 and 60 hours is represented by the shaded area in the following diagram.\\
Write down the values of a and b.
$a=\dfrac{2}{4.4}= 0.455 b=\dfrac{3}{4.4}=0.682]$

ok this was a key to a test question from 2013 but mostly I wanted to use tikz to plot the graph
also not real sure why they used the calculation they did 2 and 3 ?

no sure why this did not render here it was fine in Overleaf
also not sure even if the graph is correct
also the word noramcdf showed up on the PDF is that a mathlab or something

%preamble \usepackage{pgfplots}
\newcommand\gauss[2]{1/(#2*sqrt(2*pi))*exp(-((x-#1)^2)/(2*#2^2))} % Gauss function, parameters mu and sigma
\begin{axis}[every axis plot post/.append style={
mark=none,samples=50,smooth}, % All plots: 50 samples, smooth, no marks
axis x line*=bottom, % no box around the plot, only x axis
axis y line=none, % the * suppresses the arrow tips
enlargelimits=upper, % extend the axes a bit to the right and top
domain=-2:3, % Default for all plots: from -4:4
xtick={-.455,.655},
xticklabels={$-.455$,$.655$},
width=10cm,
height=4cm]
\addplot [fill=gray!30, draw=none, domain=-0.45:0.655] {\gauss{-0.455}{0.655}} \closedcycle;
\addplot {\gauss{-0.455}{0.655}};
\end{axis}
\end{tikzpicture}

 

[I like Serena]

It's because \begin{tikzpicture} is missing at the beginning.
When we add it, we get:
\begin{tikzpicture}
%preamble \usepackage{pgfplots}
\newcommand\gauss[2]{1/(#2*sqrt(2*pi))*exp(-((x-#1)^2)/(2*#2^2))} % Gauss function, parameters mu and sigma
\begin{axis}[every axis plot post/.append style={
mark=none,samples=50,smooth}, % All plots: 50 samples, smooth, no marks
axis x line*=bottom, % no box around the plot, only x axis
axis y line=none, % the * suppresses the arrow tips
enlargelimits=upper, % extend the axes a bit to the right and top
domain=-2:3, % Default for all plots: from -4:4
xtick={-.455,.655},
xticklabels={$-.455$,$.655$},
width=10cm,
height=4cm]
\addplot [fill=gray!30, draw=none, domain=-0.45:0.655] {\gauss{-0.455}{0.655}} \closedcycle;
\addplot {\gauss{-0.455}{0.655}};
\end{axis}
\end{tikzpicture}

 

[karush]

I should of seen that,,,,ok I added to the OP