iceice655
- 7
- 1
Misplaced Homework Thread
Hello, I was recently tested on finding the normal force at the base of a ladder leaning against a wall as well as its friction force. So this is the question from memory.
Given:
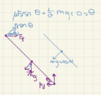
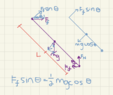
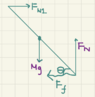
θ the acute angle between the ground and the ladder
μ as the coefficient of friction between the ground and the ladder
M as the mass of the ladder at the center of the ladder, evenly distributed so the inertia if rotated around the center is I=1/12(mL^2), and I = 1/3(mL^2) at the edges
L as the length of the ladder
Known: there is no friction between the wall and the ladder
What is the normal force at the base of the ladder and what is its friction force in terms of θ, μ, g (the gravity constant)M, and L.
Given:
θ the acute angle between the ground and the ladder
μ as the coefficient of friction between the ground and the ladder
M as the mass of the ladder at the center of the ladder, evenly distributed so the inertia if rotated around the center is I=1/12(mL^2), and I = 1/3(mL^2) at the edges
L as the length of the ladder
Known: there is no friction between the wall and the ladder
What is the normal force at the base of the ladder and what is its friction force in terms of θ, μ, g (the gravity constant)M, and L.