Normal Force in Circular Motion

[Spock2230]

Hi all,

For a marble in uniform circular motion within a smooth cone, what is the relationship between the normal force by the surface of the cone and the weight of the marble?

My take is that the normal force forms a reaction pair with one of the resolved forces of weight. I have resolved the forces in this way:

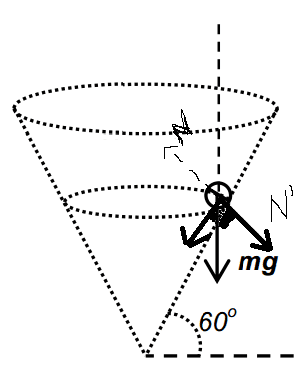(really sorry, mspaint).

However, the solutions establishes weight and the centripetal force as components of the normal contact force, which doesn't make sense to me. Here's how they resolved it.

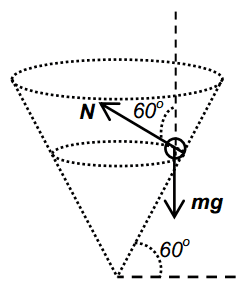
The weight of the marble, mg, is given as N cos 60 by the solution, where N is the normal contact force. The centripetal force is then given as N sin 60. This doesn't make sense to me because the normal force would be greater than the weight of the marble, when the normal force is just a reaction force to one of the components of its weight.

Anyone willing to help? Thanks in advance!

 

[Doc Al]

The normal force is not simply a reaction force to a component of the weight. Consider the net force (and acceleration) in the vertical direction.

 

[Spock2230]

Thanks for replying.
I'm rather confused about this.

http://www.regentsprep.org/Regents/physics/phys01/friction/38deg.gif
In a case like this (no circular motion), is the normal force acting as reaction force?

If it is, why would it be any different for an object in circular motion?

I understand that if you look at all the vertical components, there will be a net vertical force downwards. This means that the marble will be rolling down, which I know shouldn't be the case. And this confuses me even more.

Thanks for helping anyway!

 

[dauto]

No, the normal force is never ever ever a reaction to the weight. Keep in mind that reaction forces are forces of similar nature acting on different objects. The reaction to the normal force of the ramp on the block is the normal force of the block on the ramp. Similar nature - they are both normal forces, and different objects - one acts on the block and the other acts on the ramp. In your example you have two forces of dissimilar nature - one is a normal the other is a gravitational force, and both act on the same object - the block.

 

[Doc Al]

In a case like this (no circular motion), is the normal force acting as reaction force?

If by "reaction force" you mean a Newton's 3rd law pair to gravity, then no.

If it is, why would it be any different for an object in circular motion?

In the example without circular motion, realize that the block is accelerating down the plane. Thus it has a vertical component of acceleration. But if you examine forces perpendicular to the plane, the acceleration in that direction is zero.

In the example of circular motion there is no vertical component of acceleration. The marble is moving in a circle, not falling down the cone.

I understand that if you look at all the vertical components, there will be a net vertical force downwards. This means that the marble will be rolling down, which I know shouldn't be the case. And this confuses me even more.

No, there will not be a net vertical force. The marble executes uniform circular motion.

 

[ehild]

Hi all,

For a marble in uniform circular motion within a smooth cone, what is the relationship between the normal force by the surface of the cone and the weight of the marble?



The weight of the marble, mg, is given as N cos 60 by the solution, where N is the normal contact force. The centripetal force is then given as N sin 60. This doesn't make sense to me because the normal force would be greater than the weight of the marble, when the normal force is just a reaction force to one of the components of its weight.

Anyone willing to help? Thanks in advance!

The others explained already that the normal force is not a reaction force to one of the components of the weight. The normal force acts on the marble and it is exerted by the cone. The other force acting on the marble is gravity, mg. The reaction forces are the force of the marble pushing the cone; and the force the marble attracts the earth. You need the forces applied to the marble. The resultant force should be equal to the centripetal force which ensures moving along a horizontal circle of radius R. See attachment. From the yellow triangle, Fcp=Nsin60°, and mg =Ncos60°.

ehild

 

[Spock2230]

Thanks! I missed the fact that reaction pairs are forces of similar nature. And the diagram by ehild clears things up a lot.