Normal Modes: Finding Eigenfrequencies

In summary, normal modes are natural oscillations of a system and are important in science because they provide insights into the fundamental properties and behavior of physical systems. The eigenfrequencies of a system can be calculated by solving the eigenvalue problem, which involves finding the values that make a system vibrate at its natural frequencies. These eigenfrequencies are affected by factors such as mass, stiffness, and geometry of the system. Normal modes and eigenfrequencies are used in various fields of science, including physics, chemistry, engineering, and music. They can also be experimentally observed through techniques such as spectroscopy and modal analysis, providing valuable information about the system.
  • #1
Sum Guy
21
1
If I have a system where the following is found to describe the motion of three particles:

1zyzm8z.png

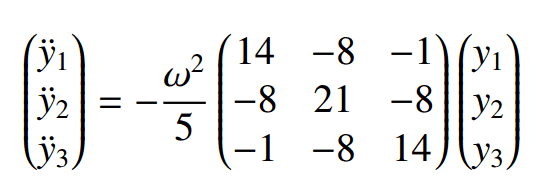
The normal modes of the system are given by the following eigenvectors: $$(1,0,-1), (1,1,1), (1,-2,1)$$
How can I find the corresponding eigenfrequencies? It should be simple... What am I missing?
 
Physics news on Phys.org
  • #2
Is this for schoolwork?
 
  • #3
berkeman said:
Is this for schoolwork?
This is something I found in a pdf online where it simply asserted what the eigenfrequencies were... and not how to find them.
 
  • Like
Likes berkeman

FAQ: Normal Modes: Finding Eigenfrequencies

What are normal modes and why are they important in science?

Normal modes refer to the natural oscillations or vibrations of a system. They are important in science because they provide insights into the fundamental properties and behavior of physical systems, such as molecules, atoms, and structures.

How do you calculate the eigenfrequencies of a system?

The eigenfrequencies of a system can be calculated by solving the eigenvalue problem, which involves finding the values of a matrix that, when multiplied by a vector, result in a scalar multiple of the vector. In simpler terms, it involves finding the values that make a system vibrate at its natural frequencies.

What factors affect the eigenfrequencies of a system?

The eigenfrequencies of a system are affected by various factors, including the mass, stiffness, and geometry of the system. An increase in mass or stiffness will result in a decrease in eigenfrequencies, while a change in geometry can lead to a change in the number of eigenfrequencies.

How are normal modes and eigenfrequencies used in different fields of science?

Normal modes and eigenfrequencies are used in a variety of fields, including physics, chemistry, engineering, and even music. In physics, they are used to study the properties of molecules and materials. In chemistry, they are used to understand the behavior of atoms and molecules. In engineering, they are used to design and analyze structures. In music, they are used to create different sounds and harmonies.

Can normal modes and eigenfrequencies be experimentally observed?

Yes, normal modes and eigenfrequencies can be experimentally observed using techniques such as spectroscopy, which measures the frequencies of electromagnetic radiation absorbed by a system, or modal analysis, which measures the natural frequencies of a structure through vibration testing. These observations can provide valuable information about the properties and behavior of a system.

Similar threads

I Error tolerant normal mode frequency
Replies
7
Views
2K
I Normal modes of vibration from the total energy
Replies
3
Views
915
Small oscillations: How to find normal modes?
Replies
4
Views
2K
I Coupled mode theory - question about an equation
Replies
1
Views
2K
Analysing the Normal Modes and Dynamics of a Cluster of Atoms
Replies
1
Views
1K
Meaning of normal coordinates and normal modes, in relation to phonons
Replies
1
Views
6K
Understanding solution to equations of motion of n coupled oscillators
Replies
4
Views
724
I How can phonons "travel" if they are excitations of normal modes?
Replies
7
Views
3K
Coupled oscillators -- period of normal modes
Replies
11
Views
2K
A Equipartition theorem and Coupled harmonic oscillator system
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top