Normalisation of the radial wavefunction in 2s state?

[ASSAem]

Okay, so I've been set this homework to find the normalisation constant, N, for the radial wave function in the 2s state for hydrogen (my title was too long to fit that vital information in). thing is; I'm having a bloody hard time and in the process confusing myself with trying to take out all constants from the integral after normalising the radial wavefunction.
we are given that the radial wavefunction in the 2s state for hydrogen is:

R₂₀(r) = N (1−r/2a₀) e^-r/a₀

where N is the normalisation constant.
Im going to attach a picture of what i have done so far, as

a)I'm new to this and have no idea how to insert formulae
b)typing it out in this way would be confusing for people...i think.

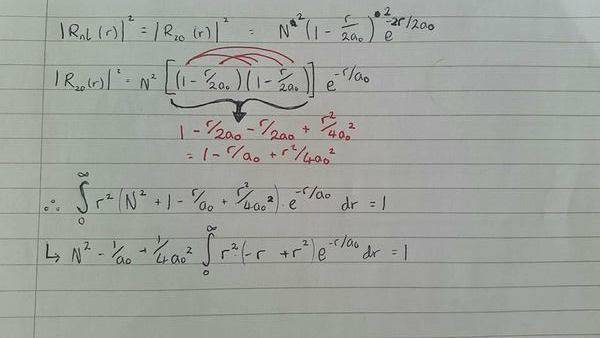
So I get to here, where I've squared out the wavefunction in order to normalise it to equal 1; and as I am integrating w.r.t. r; I need to keep those into the equation.

the problem i am having is taking out the constants a₀ and a₀²
so i tried taking it apart but i think this is incorrect.

can anyone give any advice? thank you :)

 

[DrClaude]

There are a couple of things wrong here.

First,
$$
N^2 (1 + a + b) \neq N^2 + 1 + a + b
$$

Second, you have a similar problem in the integral. $r/a_0$ cannot become $1/a_0 + r$, and so on.