Normality of errors and residuals in ordinary linear regression

[fog37]

TL;DR Summary

Checking for normality of errors and residuals in ordinary linear regression

Hello,
In reviewing the classical linear regression assumptions, one of the assumptions is that the residuals have a normal distribution...I also read that this assumption is not very critical and the residual don't really have to be Gaussian.
That said, the figure below show $Y$ values and their residuals with a normal distribution of equal variance at the $X$ value:

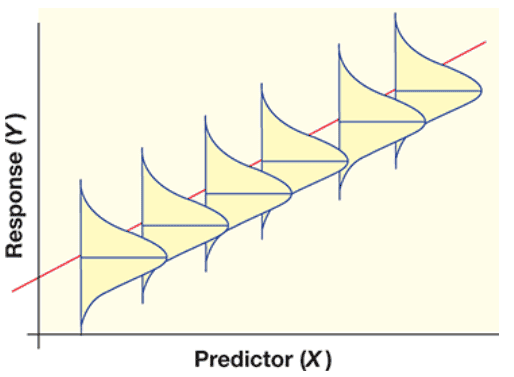
To check for residual normality, should we check the distribution of residuals at each $X$ (not very practical)? Instead, we usually plot a histogram of ALL the residuals at different X values...But that is not what the assumption is about (normality of residuals for each predictor $X$ value)...

Thank you...

 

[FactChecker]

one of the assumptions is that the residuals have a normal distribution...I also read that this assumption is not very critical

Critical for what? You should probably be careful about any probability or confidence intervals that come from a model where the random term is not normal.

and the residual don't really have to be Gaussian.

There are glaring and common examples that violate that assumption. If all the $Y$ must be positive, then a lot of the negative normal tail might be missing. If the random variance is a percentage of the $Y$ values, then a log transformation should be looked at.

That said, the figure below show $Y$ values and their residuals with a normal distribution of equal variance at the $X$ value:

View attachment 338295

To check for residual normality, should we check the distribution of residuals at each $X$ (not very practical)? Instead, we usually plot a histogram of ALL the residuals at different X values...But that is not what the assumption is about (normality of residuals for each predictor $X$ value)...

True. A lot depends on the subject matter expertise of the statistician. Does he have a valid reason to model the subject as a linear model with a random normal term?

 

[statdad]

The assumption of a Gaussian error structure is not part of the basic regression assumptions. IF that assumption is added then things like the distributions of the LS estimates are exact rather than approximate as they are without it.

When the Gaussian assumption is made it is this: the error terms are i.i.d normal with mean 0 and variance sigma squared. This links to your picture of the bell curves superimposed on the regression line as follows:
- in this case Y1 through Yn are each normally distributed with mean b0 + bx1 and variance sigma squared
- the bell curves on the regression plot don't show the distribution of the errors, it is meant to show each normal distribution of the Y values

This leads to your question: we don't need to check the error distribution for each value of x since those values don't influence the error distributions: the error distributions are, as I mentioned above, i.i.d with mean 0 and constant variance, so the checks we use on them work

You should also remember this: there is no such thing as any data that is truly normally distributed: that is an ideal, and our checks are done simply to see whether our collected data's distribution is similar enough to that of the ideal to allow us to use normal-based calculations.

 

[WWGD]

I believe, using Cochran's theorem, it justifies the distribution of the associated Anova statistics.