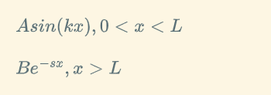Normalizing Wavefunction: Hard QM Question)

[drop_out_kid]

Homework Statement

For a well left side is infinite potential and right side is finite potential V0 , and the energy is constant and less than V0(also constant). Now get the wave function , get the equation for eigen energy(the energy allowed) and the conditions for no solution

Relevant Equations

$$-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \Phi(x)+V(x)\Phi(x)=0$$

So I have come up with my solution(attempt) which is:

where

(
$$\psi_ 1 \triangleq Asin(kx),0<x<L$$

$$\psi_ 2 \triangleq Be^{-sx},x>L$$

$$k \triangleq \sqrt{\frac{2mE}{\hbar^2}} $$

$$s \triangleq \sqrt{\frac{2m(V-E)}{\hbar^2}} $$)

But this has a serious problem about boundary: I think I should use that

But this is what I get:

So:
1. How can I get this normalisation in a easy way?
2. Can I use this for part (b) to solve eigen energy?Thought for hours , assignment is going to due (

 

[drop_out_kid]

And congratulation to myself, markdown finally worked.

 

[drop_out_kid]

Some new progress:

I still didn't find way to normalise this.. Perhaps problem doesn't require it idk, and I am analyze this equation:

$$
\alpha \triangleq\sqrt{E} \ \
\gamma \triangleq\sqrt{\frac{2m}{\hbar^2}}L \ \
tan(\gamma\alpha)=-\sqrt{\frac{\alpha^2}{V-\alpha^2}}\ \ (\gamma,V\ \ are\ \ constant)
$$

 

[kuruman]

To normalize the piecewise continuous wavefunction, express $\psi_1(x)$ and $\psi_2(x)$ in terms of a single constant, $A$ or $B$, and then normalize the usual way. The energy eigenvalues will have to be deternined graphically or numerically.

 

[drop_out_kid]

To normalize the piecewise continuous wavefunction, express $\psi_1(x)$ and $\psi_2(x)$ in terms of a single constant, $A$ or $B$, and then normalize the usual way. The energy eigenvalues will have to be deternined graphically or numerically.

But I can determine the upper bound of V by Tangent function asymptotic line right?
Not sure but I get sth like V<=Pi^2*hbar^2/(8mL)

 

[kuruman]

But I can determine the upper bound of V by Tangent function asymptotic line right?
Not sure but I get sth like V<=Pi^2*hbar^2/(8mL)

What upper bound of V? How do you propose to find the eigenvalues? Have you studied how to find them in the case of the particle in a box and in the case of a square well? This is a hybrid that combines the two methods for finding the eigenvalues.

 

[drop_out_kid]

What upper bound of V? How do you propose to find the eigenvalues? Have you studied how to find them in the case of the particle in a box and in the case of a square well? This is a hybrid that combines the two methods for finding the eigenvalues.

If V is bigger than this , there's no possible energy.(from the two eqs of B/A)

 

[kuruman]

If V is bigger than this , there's no possible energy.(from the two eqs of B/A)

What is "this" that V cannot be bigger than? V is infinite at x = 0 and you already know how to deal with that. It is -U in the region 0 ≤ x ≤ L (the well) and zero for x > L. The two equations give you $$\frac{k\cos(kL)}{-se^{-sL}}=\frac{\sin(kL)}{e^{-sL}}.$$That's what you have to solve numerically for $E$ which is implicit in the definitions for $k$ and $s$.

 

[Orodruin]

If V is bigger than this , there's no possible energy.(from the two eqs of B/A)

Why? The infinite square well has an infinite number of bound eigenstates.

 

[Orodruin]

Regarding normalization: You will always be able to normalize the wave function as long as the norm is finite (which you have already used implicitly to discard the exponentially growing solutions). The issue is instead whether solutions exist for particular energies. To find out you need to use the matching conditions in the way described by @kuruman (also obtainable by dividing one matching condition by the other). To obtain the condition for no bound state solution (there will always be a continuum of scattering states in this problem), you need to find out when the equation thus obtained has no solutions for $E < V$.