Not understanding these manipulations involving Partial Derivatives

MatinSAR
Messages
673
Reaction score
204
Homework Statement
Find partial derivatives
Relevant Equations
dy/dx=(dy/dt)(dt/dx)
Can someone please help me to find out what happened here ?

1675445974557.png
 
Physics news on Phys.org
It's differentiating ##f## with respect to its arguments, then differentiating the arguments with respect to ##t##. It might be clearer if you write ##u = tx## and ##v=ty##, then
$$\partial f(u,v) / \partial t = (\partial f/ \partial u) (\partial u/ \partial t) + (\partial f/ \partial v) (\partial v/ \partial t)$$
 
Reply
  • Like
Likes SammyS, Mark44 and MatinSAR
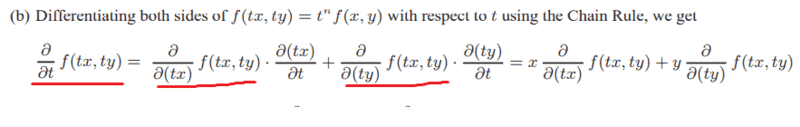
ergospherical said:
It's differentiating ##f## with respect to its arguments, then differentiating the arguments with respect to ##t##. It might be clearer if you write ##u = tx## and ##v=ty##, then
$$\partial f(u,v) / \partial t = (\partial f/ \partial u) (\partial u/ \partial t) + (\partial f/ \partial v) (\partial v/ \partial t)$$
That "tx" confused me ...
Now it's clear...
Thank you for your time 🙏🙏
 

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Thread 'Finding the nth roots of a complex number'

There are two things I don't understand about this problem. First, when finding the nth root of a number, there should in theory be n solutions. However, the formula produces n+1 roots. Here is how. The first root is simply ##\left(r\right)^{\left(\frac{1}{n}\right)}##. Then you multiply this first root by n additional expressions given by the formula, as you go through k=0,1,...n-1. So you end up with n+1 roots, which cannot be correct. Let me illustrate what I mean. For this...
View full post »

Similar threads

Multivariable calculus problem involving partial derivatives along a surface
Replies
9
Views
2K
Need a real life example where a partial derivative is used in motion
Replies
3
Views
2K
Directional derivatives vs Partial derivatives
Replies
7
Views
2K
Calculating the partial derivative in polar coordinates
Replies
3
Views
3K
Expanding Brackets with Partial Derivatives
Replies
2
Views
2K
Sign of a second partial derivative
Replies
1
Views
2K
Laplace transform of proper rational function
Replies
6
Views
1K
Calculating 2nd Total Derivative of u w.r.t. t
Replies
28
Views
3K
Differential Integration Problem
Replies
4
Views
2K
Solving Second Order Partial Derivative By Changing Variable
Replies
5
Views
4K

Hot Threads

Recent Insights

Back
Top