Notation clarification: SU(N) group integration

[paralleltransport]

Homework Statement

This is not a homework problem.

Relevant Equations

U is a matrix element of SU(N). dU is the haar measure (left invariant measure) on the SU(N) lie group.

Hello,

I would like help to clarify what det( {\delta \over \delta J}) W(J) (equation 15.79) actually means, and why it returns a number (and not a matrix). This comes from the following problem statement (Kaku, Quantum Field Theory, a Modern Introduction)

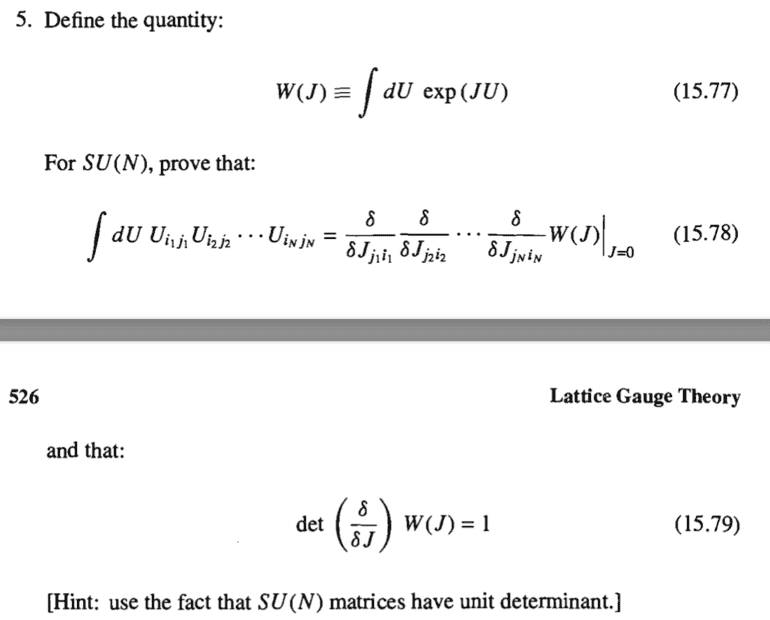
Naively, one would define det ({\delta \over \delta J}) W(J) to be the determinant of the matrix whose i, j'th element is
δWδJijδWδJij

 

[samalkhaiat]

I would like help to clarify what $\det(\frac{\delta }{\delta J}) W(J)$.

The determinant of any $n \times n$ matrix (such as $u$ and $\frac{\delta}{\delta J}$) is given by $$\det (M) = \frac{1}{n!} \epsilon_{i_{1} \cdots i_{n}} \ \epsilon_{j_{1} \cdots j_{n}} \ M_{i_{1}j_{1}} \ \cdots \ M_{i_{n}j_{n}} .$$ Now take $M = u \in SU(n)$ and integrate over $SU(n)$: since $\det (u) = 1$ and the measure is normalized $\int_{SU(n)} d \mu (u) = 1$, you get $$1 = \frac{1}{n!} \epsilon_{i_{1} \cdots i_{n}} \ \epsilon_{j_{1} \cdots j_{n}} \int_{SU(n)} d \mu (u) \ u_{i_{1}j_{1}} \ \cdots \ u_{i_{n}j_{n}} ,$$ or $$1 = \left( \frac{1}{n!} \epsilon_{i_{1} \ \cdots \ i_{n}} \ \epsilon_{j_{1} \ \cdots \ j_{n}} \frac{\delta}{\delta J_{i_{1}j_{1}}} \ \cdots \frac{\delta}{\delta J_{i_{n}j_{n}}} \right) W(J) \equiv \mbox{det}(\frac{\delta}{\delta J}) W(J) .$$

 

[paralleltransport]

OK that clears it up thanks!