Evgeny.Makarov
Gold Member
MHB
- 2,434
- 4
Sorry for a long post. I am looking for a clear and concise way to explain how to compute coordinates when changes of basis or linear operators are involved. I would like to avoid the summation notation as much as possible and use the definition of matrix multiplication only in the beginning, when it is indeed necessary. I would like to be able to explain things like the following.
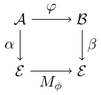
While it is possible to explain the change of basis referring to "new" and "old" coordinates of a single vector in two bases, applying an operator $\varphi$ to a vector $v$ involves four sets of coordinates:
A popular idea is to write $[v]_{\mathcal{E}}$ to refer to coordinates of vector $v$ in basis $\mathcal{E}$. Similarly, $[\varphi]_{\mathcal{E}}$ denotes the matrix of $\varphi$ in $\mathcal{E}$ and if $\mathcal{E}'=(e_1',\dots,e_n')$, then $[\mathcal{E}']_{\mathcal{E}}$ is the matrix with columns $[e_1']_{\mathcal{E}},\dots,[e_n']_{\mathcal{E}}$, i.e., the transition matrix from $\mathcal{E}$ to $\mathcal{E}'$. By definition,
\[
[\varphi]_{\mathcal{E}}=[\varphi\mathcal{E}]_{\mathcal{E}}.\tag{1}
\]
Then we can state and prove the following properties.
\begin{align}
&[\mathcal{E}']_{\mathcal{E}}[v]_{\mathcal{E}'}=[v]_{\mathcal{E}}\tag{2}\\
&[v]_{\mathcal{E}}=[\varphi v]_{\mathcal{\varphi E}}\tag{3}
\end{align}
Using this, we can prove that
\[
[\varphi v]_{\mathcal{E}}=[\varphi]_{\mathcal{E}}[v]_{\mathcal{E}}.\tag{4}
\]
Indeed,
\[
[\varphi v]_{\mathcal{E}}\overset{(2)}{=}[\varphi\mathcal{E}]_{\mathcal{E}}[\varphi v]_{\mathcal{\varphi E}}
\overset{(1)}{=}[\varphi]_{\mathcal{E}}[\varphi v]_{\varphi\mathcal{E}}\overset{(3)}{=}[\varphi]_{\mathcal{E}}[v]_{\mathcal{E}}.\tag{5}
\]
For another example, here is the summary of Deveno's explanation that $[\varphi]_{\mathcal{E}'}=[\mathcal{E}]_{\mathcal{E}'}[\varphi]_{\mathcal{E}}[\mathcal{E}']_{\mathcal{E}}$ https://driven2services.com/staging/mh/index.php?posts/55983/. For any $v$,
\[
[\mathcal{E}]_{\mathcal{E}'}[\varphi]_{\mathcal{E}}[\mathcal{E}']_{\mathcal{E}}[v]_{\mathcal{E}'}
\overset{(2)}{=}
[\mathcal{E}]_{\mathcal{E}'}[\varphi]_{\mathcal{E}}[v]_{\mathcal{E}}
\overset{(4)}{=}
[\mathcal{E}]_{\mathcal{E}'}[\varphi v]_{\mathcal{E}}
\overset{(2)}{=}
[\varphi v]_{\mathcal{E}'}.
\]
This notation seems short and expressive, but unfortunately $[v]_{\mathcal{E}}$ does not make sense if $\mathcal{E}$ is not a basis. So if $\varphi$ is not an isomorphism, then the proof (5) does not quite work.
It is possible to define the inverse operation: if $x$ is a column of numbers, then $(x)_{\mathcal{E}}\overset{\text{def}}{=}\mathcal{E}x$ is the linear combination of vectors from $\mathcal{E}$ with coefficients $x$. This operation is well-defined even if $\mathcal{E}$ are linearly dependent. I have not yet finished rewriting (1)-(4) using this notation, but even if this is possible, I am wondering if the proofs would not be too obscure and giving little insight.
How do authors and lecturers usually deal with this? Also, I am wondering if there is a generalization of the operation of taking coordinates. Perhaps coordinates can be thought of as a morphism in category theory from $V\times\dots\times V$ to $V$ taking a basis into a vector. Maybe such a generalization can give a hint for a suitable notation.
Thank you.
- Why is it that when a change of basis occurs, we express the "old" coordinates through the "new" ones, but when a linear operator is applied, we express the "new" coordinates through the "old" ones?
- How to find the matrix of a linear operator in a different basis?
- Suppose a linear operator $\varphi$ on $\Bbb R^n$ maps a sequence of vectors $\mathcal{A}=(a_1,\dots,a_n)$ to $\mathcal{B}=(b_1,\dots,b_n)$ and $\mathcal{A}$ is linear independent. How to find the matrix of $\varphi$ in basis $\mathcal{E}$ given coordinates of $\mathcal{A}$ and $\mathcal{B}$ in $\mathcal{E}$?
While it is possible to explain the change of basis referring to "new" and "old" coordinates of a single vector in two bases, applying an operator $\varphi$ to a vector $v$ involves four sets of coordinates:
- coordinates of $v$ in the initial basis $\mathcal{E}$,
- coordinates of $\varphi v$ in the initial basis $\mathcal{E}$,
- coordinates of $v$ in the new basis $\varphi\mathcal{E}$ and
- coordinates of $\varphi v$ in the new basis $\varphi\mathcal{E}$.
A popular idea is to write $[v]_{\mathcal{E}}$ to refer to coordinates of vector $v$ in basis $\mathcal{E}$. Similarly, $[\varphi]_{\mathcal{E}}$ denotes the matrix of $\varphi$ in $\mathcal{E}$ and if $\mathcal{E}'=(e_1',\dots,e_n')$, then $[\mathcal{E}']_{\mathcal{E}}$ is the matrix with columns $[e_1']_{\mathcal{E}},\dots,[e_n']_{\mathcal{E}}$, i.e., the transition matrix from $\mathcal{E}$ to $\mathcal{E}'$. By definition,
\[
[\varphi]_{\mathcal{E}}=[\varphi\mathcal{E}]_{\mathcal{E}}.\tag{1}
\]
Then we can state and prove the following properties.
\begin{align}
&[\mathcal{E}']_{\mathcal{E}}[v]_{\mathcal{E}'}=[v]_{\mathcal{E}}\tag{2}\\
&[v]_{\mathcal{E}}=[\varphi v]_{\mathcal{\varphi E}}\tag{3}
\end{align}
Using this, we can prove that
\[
[\varphi v]_{\mathcal{E}}=[\varphi]_{\mathcal{E}}[v]_{\mathcal{E}}.\tag{4}
\]
Indeed,
\[
[\varphi v]_{\mathcal{E}}\overset{(2)}{=}[\varphi\mathcal{E}]_{\mathcal{E}}[\varphi v]_{\mathcal{\varphi E}}
\overset{(1)}{=}[\varphi]_{\mathcal{E}}[\varphi v]_{\varphi\mathcal{E}}\overset{(3)}{=}[\varphi]_{\mathcal{E}}[v]_{\mathcal{E}}.\tag{5}
\]
For another example, here is the summary of Deveno's explanation that $[\varphi]_{\mathcal{E}'}=[\mathcal{E}]_{\mathcal{E}'}[\varphi]_{\mathcal{E}}[\mathcal{E}']_{\mathcal{E}}$ https://driven2services.com/staging/mh/index.php?posts/55983/. For any $v$,
\[
[\mathcal{E}]_{\mathcal{E}'}[\varphi]_{\mathcal{E}}[\mathcal{E}']_{\mathcal{E}}[v]_{\mathcal{E}'}
\overset{(2)}{=}
[\mathcal{E}]_{\mathcal{E}'}[\varphi]_{\mathcal{E}}[v]_{\mathcal{E}}
\overset{(4)}{=}
[\mathcal{E}]_{\mathcal{E}'}[\varphi v]_{\mathcal{E}}
\overset{(2)}{=}
[\varphi v]_{\mathcal{E}'}.
\]
This notation seems short and expressive, but unfortunately $[v]_{\mathcal{E}}$ does not make sense if $\mathcal{E}$ is not a basis. So if $\varphi$ is not an isomorphism, then the proof (5) does not quite work.
It is possible to define the inverse operation: if $x$ is a column of numbers, then $(x)_{\mathcal{E}}\overset{\text{def}}{=}\mathcal{E}x$ is the linear combination of vectors from $\mathcal{E}$ with coefficients $x$. This operation is well-defined even if $\mathcal{E}$ are linearly dependent. I have not yet finished rewriting (1)-(4) using this notation, but even if this is possible, I am wondering if the proofs would not be too obscure and giving little insight.
How do authors and lecturers usually deal with this? Also, I am wondering if there is a generalization of the operation of taking coordinates. Perhaps coordinates can be thought of as a morphism in category theory from $V\times\dots\times V$ to $V$ taking a basis into a vector. Maybe such a generalization can give a hint for a suitable notation.
Thank you.