- #1
Prove It
Gold Member
MHB
- 1,465
- 24
View attachment 5628
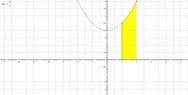
Here is a sketch of the region to be rotated.
View attachment 5629
To find a volume using cylindrical shells, you first need to picture what the region would like like when that area is rotated around the y axis. Then consider how it would look if that solid was made up of very thin cylinders.
Each cylinder has a curved area that is a rectangle (rotated around to form the cylinder), which has area $\displaystyle \begin{align*} 2\,\pi\,r\,h \end{align*}$, and in this case, the radius of the cylinder is the x value, and the height of the cylinder is the y value. So the area of the curved surface of each cylinder is $\displaystyle \begin{align*} 2\,\pi\,x\,y \end{align*}$, and so the volume of each cylinder is $\displaystyle \begin{align*} 2\,\pi\,x\,y\,\Delta x \end{align*}$, where $\displaystyle \begin{align*} \Delta x \end{align*}$ is a small change in x.
Thus we can approximate the total volume by summing the volumes of all these cylinders, i.e.
$\displaystyle \begin{align*} V \approx \sum{ 2\,\pi\,x\,y\,\Delta x } \end{align*}$
To improve on the approximation, we increase the number of cylinders. As we make the number of cylinders $\displaystyle \begin{align*} n \to \infty \end{align*}$ and $\displaystyle \begin{align*} \Delta x \to 0 \end{align*}$, the approximation becomes exact and the sum becomes an integral. Thus
$\displaystyle \begin{align*} V &= \int_1^2{ 2\,\pi\,x\,y\,\mathrm{d}x } \\ &= 2\,\pi\int_1^2{x\,\left( 2 + \frac{1}{2}\,x^2 \right) \,\mathrm{d}x } \\ &= 2\,\pi\int_1^2{ \left( 2\,x + \frac{1}{2}\,x^3 \right) \,\mathrm{d}x } \\ &= 2\,\pi\,\left[ x^2 + \frac{1}{8}\,x^4 \right] _1^2 \\ &= 2\,\pi\,\left\{ \left[ 2^2 + \frac{1}{8}\,\left( 2 \right) ^4 \right] - \left[ 1^2 + \frac{1}{8}\,\left( 1 \right) ^4 \right] \right\} \\ &= 2\,\pi\,\left[ \left( 4 + 2 \right) - \left( 1 + \frac{1}{8} \right) \right] \\ &= 2\,\pi\,\left( \frac{39}{8} \right) \\ &= \frac{39\,\pi}{4}\,\textrm{units}^3 \end{align*}$
Here is a sketch of the region to be rotated.
View attachment 5629
To find a volume using cylindrical shells, you first need to picture what the region would like like when that area is rotated around the y axis. Then consider how it would look if that solid was made up of very thin cylinders.
Each cylinder has a curved area that is a rectangle (rotated around to form the cylinder), which has area $\displaystyle \begin{align*} 2\,\pi\,r\,h \end{align*}$, and in this case, the radius of the cylinder is the x value, and the height of the cylinder is the y value. So the area of the curved surface of each cylinder is $\displaystyle \begin{align*} 2\,\pi\,x\,y \end{align*}$, and so the volume of each cylinder is $\displaystyle \begin{align*} 2\,\pi\,x\,y\,\Delta x \end{align*}$, where $\displaystyle \begin{align*} \Delta x \end{align*}$ is a small change in x.
Thus we can approximate the total volume by summing the volumes of all these cylinders, i.e.
$\displaystyle \begin{align*} V \approx \sum{ 2\,\pi\,x\,y\,\Delta x } \end{align*}$
To improve on the approximation, we increase the number of cylinders. As we make the number of cylinders $\displaystyle \begin{align*} n \to \infty \end{align*}$ and $\displaystyle \begin{align*} \Delta x \to 0 \end{align*}$, the approximation becomes exact and the sum becomes an integral. Thus
$\displaystyle \begin{align*} V &= \int_1^2{ 2\,\pi\,x\,y\,\mathrm{d}x } \\ &= 2\,\pi\int_1^2{x\,\left( 2 + \frac{1}{2}\,x^2 \right) \,\mathrm{d}x } \\ &= 2\,\pi\int_1^2{ \left( 2\,x + \frac{1}{2}\,x^3 \right) \,\mathrm{d}x } \\ &= 2\,\pi\,\left[ x^2 + \frac{1}{8}\,x^4 \right] _1^2 \\ &= 2\,\pi\,\left\{ \left[ 2^2 + \frac{1}{8}\,\left( 2 \right) ^4 \right] - \left[ 1^2 + \frac{1}{8}\,\left( 1 \right) ^4 \right] \right\} \\ &= 2\,\pi\,\left[ \left( 4 + 2 \right) - \left( 1 + \frac{1}{8} \right) \right] \\ &= 2\,\pi\,\left( \frac{39}{8} \right) \\ &= \frac{39\,\pi}{4}\,\textrm{units}^3 \end{align*}$