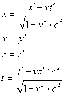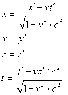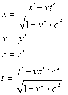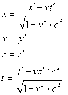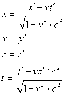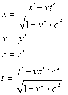Now it remains to be shown that A = B. I'll leave that to you.

[Nitric]

1. Start with the expression x'^2 + y'^2 _ z'^2 -c^2t'^2 and show, with the aid of the Lorentz transofmration, that this quantity is equal to x^2 + y^2 + z^2 -c^2t^2. This result establishes the invariance of s^2 defined by s^2 = x^2 + y^2 + z^2 -c^2t^2



2. s^2 = x^2 + y^2 + z^2 -c^2t^2



3. So far I have y = y' and z = z' because of the transformation law. basically there is no lorentz contraction perpendicular to the motion of X so y = y' and z = z'

how do i really solve this problem? where should I start?

 

[CompuChip]

So what does the Lorentz transformation look like for x' and t', in terms of x and t?
I mean, what is the correct full expression for

t' = ... t + ... x
x' = ... x + ... t
y' = y
z' = z

 

[Nitric]

 

[CompuChip]

Very nice. It's straightforward algebra then: plug them into
$x^2 - c^2 t^2$
and show that you can simplify it to
$(x')^2 - c^2 (t')^2$.

 

[Nitric]

Very nice. It's straightforward algebra then: plug them into
$x^2 - c^2 t^2$
and show that you can simplify it to
$(x')^2 - c^2 (t')^2$.

so I would have
(x'+vt'/sqrt(1-v^2/c^2)^2 - c^2(t' + vx'/c^2 / sqrt(1-v^2/c^2) and simplify it algebraically to x'^2 - c^2t'^2 ?

 

[CompuChip]

Yes, the expression is a bit unclear, but it looks like what I got,
$$\frac{(x' + v t')^2 - (t' + v x' / c^2)^2}{(\sqrt{1 - v^2/c^2)^2}$$
Just work out the multiplication (don't forget the cross-term). Then you'll see some cancellation taking place and you can factor the rest into something$\,{}\times (x'^2 - c^2t'^2)$.

 

[Nitric]

thanks a lot, i will get on this now :D

 

[Nitric]

I'm sort of stuck, my algebra isn't as fresh as I thought it would be. But am I on the right track though?

http://img264.imageshack.us/img264/1081/1233176495203dl2.jpg

^ My work

 

[CompuChip]

You are on the right track, I see two terms cancelling.
Watch the squares however, I see c^2 t'^2 instead of (c^2 t')^2 and v x'^2 instead of (v x')^2...

Also it may help to write everything in one fraction.

 

[Nitric]

I need a common denominator to start canceling things out right, or can I do it before? This is the part where my algebra isn't as fresh as it should be. To get the common denominator, I have to multiply the left equation by c^4 (top and bottom) and multiple the right equation by 1 (top and bottom) correct?

 

[Nitric]

Okay I did what I said on the previous post and so far I have:

c^4[x'^2 + (vt')^2] - (c^2t')^2 - (vx'^2) / c^4(1-v^2/c^2)

What can I do now to move forward? I don't see anything else cancel out.

 

[Nitric]

Okay my way isn't right, still stuck on this :|

 

[CompuChip]

It seems you're having a little problem with the algebra. Let me get you started.

Since y' = y and z' = z, it suffices to show that x'^2 - c^2 t'^2 = x^2 - c^2 t^2.
Plugging it in:

$$x^2 - c^2 t^2 = \left( \frac{ x' + v t' }{ \sqrt{1 - v^2 / c^2} } \right)^2 - c^2 \left( \frac{ t' + v x' / c^2 }{ \sqrt{1 - v^2 / c^2} } \right)^2.$$
Let me take the c^2 in the second term inside the brackets (c^2 a^2 = (c a)^2) and take the square root outside ( (a/b)^2 = a^2 / b^2, sqrt(a)^2 = a):
$$x^2 - c^2 t^2 = \frac{ \left( x' + v t' \right)^2 - \left( c t' + v x' / c \right)^2 }{ 1 - v^2 / c^2 }.$$
Open up the brackets:
$$x^2 - c^2 t^2 = \frac{ x'^2 + 2 x' v t' + v^2 t'^2 - c^2 t'^2 - 2 t' v x' - v^2 x'^2 / c^2 }{ 1 - v^2 / c^2 }.$$

Two terms cancel, after tracing the above steps carefully (make sure you understand which manipulations I did and that I didn't make any sign errors ) collect the terms in (x')^2 and (t')^2, i.e. write
$$x^2 - c^2 t^2 = \frac{ A x'^2 + B t'^2 }{ 1 - v^2 / c^2 }.$$