- #1
mt91
- 15
- 0
I was wondering if anyone could help me clarify which null cline solutions are correct for this question I've got:
I've got two differential equations:
\[ du/dt =u(1-u)(a+u)-uv \]
\[ dv/dt = buv-cv \]
where a, b and c are constants.
I know to find the u null clines you set du/dt to 0.
\[ 0=u(1-u)(a+u)-uv \]
At this stage I know u=0 is a solution. However I'm not sure for the next null cline do I find it in terms of u or v?
So is it\[ v=-u^2 -au+u+a \]
or
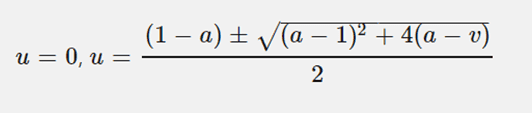
Any help would be great, cheers
I've got two differential equations:
\[ du/dt =u(1-u)(a+u)-uv \]
\[ dv/dt = buv-cv \]
where a, b and c are constants.
I know to find the u null clines you set du/dt to 0.
\[ 0=u(1-u)(a+u)-uv \]
At this stage I know u=0 is a solution. However I'm not sure for the next null cline do I find it in terms of u or v?
So is it\[ v=-u^2 -au+u+a \]
or
Any help would be great, cheers