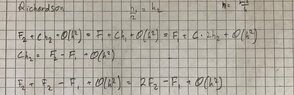Numerical Analysis - Richardson Extrapolation on Riemann Sum

In summary, numerical analysis is a field of mathematics that uses algorithms and computer methods to solve mathematical problems. The Richardson extrapolation method is a numerical technique that improves the accuracy of approximations by using a sequence of approximations with different step sizes. In the context of Riemann sums, Richardson extrapolation involves combining two different step sizes to get a more precise result. It has the advantage of reducing computational time and resources, but may not work well for certain types of functions or with large step sizes.
  • #1
Graham87
70
16
Homework Statement
Apply Richardson Extrapolation on a definite integral using Riemann sum.
Then prove that it has the same order of convergence as Trapezoidal rule.
Relevant Equations
Richardson Extrapolation
Riemann Sum
I got something like this, but I'm not sure it is correct, because if it has the same order of convergence as trapezoidal rule which is 2, it should yield the same result as trapezoidal rule but mine doesn't (?).

For example sin(x) for [0,1], n with trapezoidal rule = 0.420735...
With my own formula I get 0 or much above 0.4207.Cheers!
 

Attachments

  • 1.jpg
    1.jpg
    22.4 KB · Views: 124
Physics news on Phys.org
  • #2
Having the same order of convergence does not mean that they will necessarily give the same result. Those are two different things. They should converge to the same value and at the same rate, but may not agree along the way.
 
Last edited:
  • Informative
  • Like
Likes Graham87 and Delta2

FAQ: Numerical Analysis - Richardson Extrapolation on Riemann Sum

What is numerical analysis?

Numerical analysis is a branch of mathematics that deals with the development and implementation of methods for solving mathematical problems using numerical approximations.

What is Richardson extrapolation?

Richardson extrapolation is a numerical technique used to improve the accuracy of a numerical method by combining multiple approximations with different step sizes.

What is Riemann sum?

Riemann sum is a method for approximating the area under a curve by dividing the region into smaller rectangles and summing their areas.

How does Richardson extrapolation work on Riemann sum?

Richardson extrapolation on Riemann sum involves using a series of Riemann sums with different step sizes and then combining them to get a more accurate approximation of the area under the curve.

What are the applications of Richardson extrapolation on Riemann sum?

Richardson extrapolation on Riemann sum is commonly used in numerical integration, which has applications in various fields such as physics, engineering, and economics.

Similar threads

Calculus 2 for Engineers: Riemann sums
Replies
6
Views
1K
I Taming a Divergent Series -- But how does it work?
Replies
14
Views
2K
Advanced numerical analysis - numerical integration
Replies
2
Views
2K
Integral Question (Riemann Sums)
Replies
3
Views
3K
Compute genus via Riemann-Hurwitz and monodromy
Replies
1
Views
2K
Geometric sum using complex numbers
Replies
4
Views
2K
Solving Riemann Sums: a=3,b=8 & a=5,b=10, What is f(x) & g(x)?
Replies
2
Views
2K
Numerical Analysis: Evaluating in a numerically stable fashion
Replies
1
Views
2K
I On deriving the (inverse) Fourier transform from Fourier series
Replies
4
Views
1K
Generalising theta transformation formula from 1-d to m-d
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top