- #1
Taylor_1989
- 402
- 14
I am very new too Matlab and how it all works but I am having trouble understanding at what axis the numerical integration is occurring from on the graph that I plotted.
So I am currently doing an experiment in gamma ray spectroscopy and due to issue with the software we found it hard to integrate under a specific photo peak so it was suggest to use Matlab to integrate under the area, but the photo peak is off the x-axis so which I have highlighted in my picture below.

But my issue is I don't know how to integrate that specific area in Matlab, so what I have done so far is cherry pick the data and fit a Gaussian to it which produced the given function and graph.
Firstly here is my data set I picked for the curve
1117.4 7
1120.4 9
1123.4 7
1126.4 13
1129.4 6
1132.4 14
1135.4 15
1138.4 11
1141.4 20
1144.4 16
1147.5 16
1150.5 18
1153.5 33
1156.5 20
1159.5 19
1162.5 24
1165.5 35
1168.5 35
1171.5 43
1174.5 42
1177.5 40
1180.5 38
1183.5 38
1186.5 37
1189.5 34
1192.5 39
1195.5 34
1198.5 25
1201.6 23
1204.6 23
1207.6 19
1210.6 19
1213.6 13
1216.6 10
1219.6 16
1222.6 10
1225.6 6
1228.6 2
1231.6 11
1234.6 11
1237.6 5
1240.6 7
Next here is my code to plot the data
Ignore comment out parts I am currently experimenting
this produced the following graph
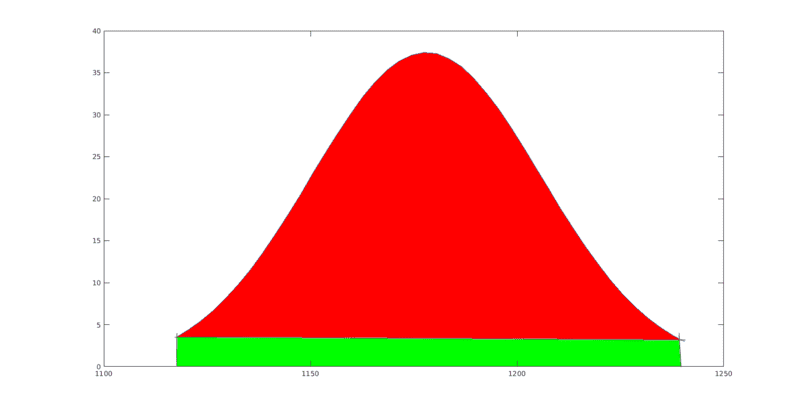

so now this is the part hat get confusing for me I need to calculate the area in the red but when i used the trapz(x,y) I think it is finding the area of both red and green, my only option at the moment I think is to shift the graph down so it aligns with the x=0 axis and it should integrate just the red area is this correct?
So I am currently doing an experiment in gamma ray spectroscopy and due to issue with the software we found it hard to integrate under a specific photo peak so it was suggest to use Matlab to integrate under the area, but the photo peak is off the x-axis so which I have highlighted in my picture below.
But my issue is I don't know how to integrate that specific area in Matlab, so what I have done so far is cherry pick the data and fit a Gaussian to it which produced the given function and graph.
Firstly here is my data set I picked for the curve
1117.4 7
1120.4 9
1123.4 7
1126.4 13
1129.4 6
1132.4 14
1135.4 15
1138.4 11
1141.4 20
1144.4 16
1147.5 16
1150.5 18
1153.5 33
1156.5 20
1159.5 19
1162.5 24
1165.5 35
1168.5 35
1171.5 43
1174.5 42
1177.5 40
1180.5 38
1183.5 38
1186.5 37
1189.5 34
1192.5 39
1195.5 34
1198.5 25
1201.6 23
1204.6 23
1207.6 19
1210.6 19
1213.6 13
1216.6 10
1219.6 16
1222.6 10
1225.6 6
1228.6 2
1231.6 11
1234.6 11
1237.6 5
1240.6 7
Next here is my code to plot the data
Code:
dataset = xlsread('Lab 3 Results 11.10.18 (1).xlsx','Sheet3','C390:D431');
x=dataset(:,1);
%y=dataset(:,2);
%plot(x,y,'-')
a1=37.43 ;
b1=1178 ;
c1=39.28 ;
d1=0
y=a1*exp(-((x-b1)/c1).^2)-d1;
%int1=trapz(x,y)
%int2=trapz(y)
plot(x,y)
%xlabel('Energy : KeV', 'FontSize', 15)
%ylabel('Number Of Interactions','FontSize', 15)Ignore comment out parts I am currently experimenting
this produced the following graph
so now this is the part hat get confusing for me I need to calculate the area in the red but when i used the trapz(x,y) I think it is finding the area of both red and green, my only option at the moment I think is to shift the graph down so it aligns with the x=0 axis and it should integrate just the red area is this correct?
