Numerical solution of a differential equation with time dependent terms

[Carlos Criollo]

I am would like to solve this differential equation:

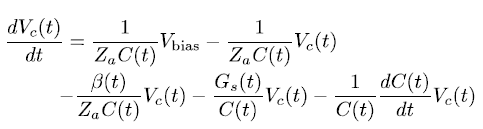
Where

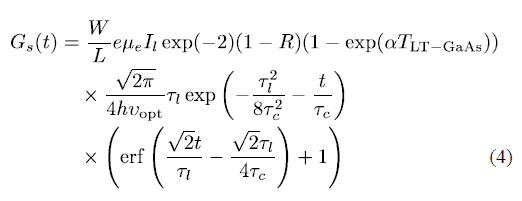
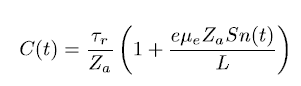
http://ieeexplore.ieee.org.ezproxy.uniandes.edu.co:8080/ielx5/8/6493417/6409989/html/img/6409989-eqdisp-3-small.png

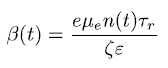
Could you give me some practical ideas about the required software and methodology? Thank you very much

 

[mfb]

If all the parameters are known, did you try to just calculate it time steps by time step? Did it work?
There are more precise integration methods, but that is something you can have a look at afterwards.

 

[Carlos Criollo]

Yes, all the parameters are known, but how I can calculate the time step by time step?

 

[SteamKing]

Yes, all the parameters are known, but how I can calculate the time step by time step?

Time is the independent variable. You start your calculations at t = 0, increment t, rinse and repeat.

 

[Carlos Criollo]

And how I could implement it in software?, I need a numerical solution of this equations.

 

[SteamKing]

There are a number of different numerical techniques for solving differential equations. The Runge-Kutta method gives reasonable accuracy without too much calculation:

http://en.wikipedia.org/wiki/Runge–Kutta_methods