- #1
giograf
- 2
- 0
[Edited]
Suppose we have two objects: (1) object number one with an observer onboard and (2) the Earth (with an observer onboard).
Object #1 is moving with speed which is reasonably close to the speed of light, the object has mass, and is moving relative to the Earth. Two systems are considered equivalent, therefore, it can be said that the Earth is moving with the speed close to the speed of light with respect to the object #1.
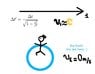
The formula for time dilation is known, so that observers in both systems can measure how differently time flows in their systems relatively to one another.
Both observers would observe that time flows slowlier in a system which is different from where they are.
But what does happen when they stop? If the systems are equivalent then time must get to the state where it was before the object #1 started to travel with the speed close to the speed of light. And not only (1) the difference in time measured before and after the travel by two observers must be exactly the same, but also (2) the change in time (between the start of the trip with the speed of light and it's end) in system #1 as perceived from the Earth!
How can it possibly be so that as long as the object #1 was moving with speed of light we had been seeing time there flowing so slowly, but when it stopped, boom. The time in both systems was the same. Did the flow at which time flows in system #1 as perceived from the Earth get an almost infinite acceleration at the moment the object #1 stopped? (If not so, why if systems are equivalent?).
Suppose we have two objects: (1) object number one with an observer onboard and (2) the Earth (with an observer onboard).
Object #1 is moving with speed which is reasonably close to the speed of light, the object has mass, and is moving relative to the Earth. Two systems are considered equivalent, therefore, it can be said that the Earth is moving with the speed close to the speed of light with respect to the object #1.
The formula for time dilation is known, so that observers in both systems can measure how differently time flows in their systems relatively to one another.
Both observers would observe that time flows slowlier in a system which is different from where they are.
But what does happen when they stop? If the systems are equivalent then time must get to the state where it was before the object #1 started to travel with the speed close to the speed of light. And not only (1) the difference in time measured before and after the travel by two observers must be exactly the same, but also (2) the change in time (between the start of the trip with the speed of light and it's end) in system #1 as perceived from the Earth!
How can it possibly be so that as long as the object #1 was moving with speed of light we had been seeing time there flowing so slowly, but when it stopped, boom. The time in both systems was the same. Did the flow at which time flows in system #1 as perceived from the Earth get an almost infinite acceleration at the moment the object #1 stopped? (If not so, why if systems are equivalent?).
Attachments
Last edited: