- #1
karush
Gold Member
MHB
- 3,269
- 5
it seems most oblique asymptotes are mostly with rational expressions but
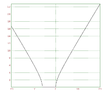
$\sqrt{x^2+6x}$ has the asymptote of $y=x+3$ and $y=-x-3$
I don't know how this is derived since it is not a rational expression
thanks ahead
$\sqrt{x^2+6x}$ has the asymptote of $y=x+3$ and $y=-x-3$
I don't know how this is derived since it is not a rational expression
thanks ahead