evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
According to my notes:
For the solution of problems with differential equations it is often useful to expand to a Fourier series with period $2L$ a function $f$ that is initially only defined on the interval $[0,L]$. We could
Suppose that we have the function $f(x)=2-x, 0<x<2$.
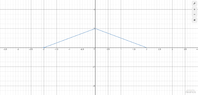
Then we get the following even and odd extension respectively:$g(x)=\left\{\begin{matrix}
2-x & , 0 \leq x \leq 2\\
2+x &, -2 <x<0\\
\end{matrix}\right.$
and
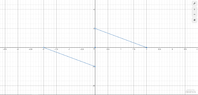
$h(x)=\left\{\begin{matrix}
2-x &,0<x<2 \\
0 & , x=0,2\\
-2+x & ,-2<x<0
\end{matrix}\right.$
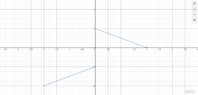
Right?The graphs of the even and odd extension of $f$ will then be the following, respectively:View attachment 6577
View attachment 6576
Am I right?
According to my notes:
For the solution of problems with differential equations it is often useful to expand to a Fourier series with period $2L$ a function $f$ that is initially only defined on the interval $[0,L]$. We could
- define a function $g$ with period $2L$ such that $g(x)=\left\{\begin{matrix}
f(x) & ,0 \leq x \leq L,\\
f(-x) & ,-L<x<0
\end{matrix}\right.$.
So the function $g$ is the even extension of $f$.
- We could also define a function $h$ with period $2L$ such that $h(x)=\left\{\begin{matrix}
f(x) & ,0 < x <L,\\
0 & , x=0,L \\
-f(-x) & ,-L<x<0
\end{matrix}\right.$.
So the function $h$ is the odd extension of $f$.
Suppose that we have the function $f(x)=2-x, 0<x<2$.
Then we get the following even and odd extension respectively:$g(x)=\left\{\begin{matrix}
2-x & , 0 \leq x \leq 2\\
2+x &, -2 <x<0\\
\end{matrix}\right.$
and
$h(x)=\left\{\begin{matrix}
2-x &,0<x<2 \\
0 & , x=0,2\\
-2+x & ,-2<x<0
\end{matrix}\right.$
Right?The graphs of the even and odd extension of $f$ will then be the following, respectively:View attachment 6577
View attachment 6576
Am I right?