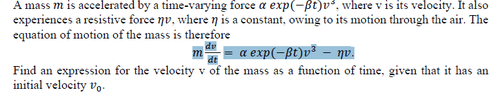ODE Methods for Physicists (related question)

[profgabs05]

Homework Statement

A mass 𝑚 is accelerated by a time-varying force 𝛼 𝑒𝑥𝑝(−𝛽𝑡)𝑣3, where v is its velocity. It also experiences a resistive force 𝜂𝑣, where 𝜂 is a constant, owing to its motion through the air. The equation of motion of the mass is therefore
𝑚𝑑𝑣/𝑑𝑡= 𝛼 𝑒𝑥𝑝(−𝛽𝑡)𝑣^3 − 𝜂𝑣.
Find an expression for the velocity v of the mass as a function of time, given that it has an initial velocity 𝑣0

Relevant Equations

𝑚𝑑𝑣/𝑑𝑡= 𝛼 𝑒𝑥𝑝(−𝛽𝑡)𝑣^3 − 𝜂𝑣.

 

[Chestermiller]

$$\frac{1}{v^3}\frac{dv}{dt}=-\frac{1}{2}\frac{dv^{-2}}{dt}$$

 

[profgabs05]

Please can i get a working guide to this answer

$$\frac{1}{v^3}\frac{dv}{dt}=-\frac{1}{2}\frac{dv^{-2}}{dt}$$

Please can i get a working guide to this answer?

 

[Chestermiller]

Please can i get a working guide to this answer
Please can i get a working guide to this answer?

$$\frac{dx^n}{dx}=nx^{n-1}$$

 

[Fred Wright]

You can solve this ODE using an integrating factor. Please see https://tutorial.math.lamar.edu/classes/de/linear.aspx.
Edit: Aerodynamic force varies as the square of the velocity NOT the cube.