Offset Torque: Solving the 1000N Problem

[DarkBlitz]

Hello guys,

I am doing some basic design work and can't remember how offset torques work.

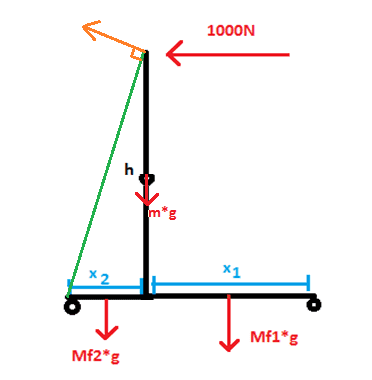
I am doing the sum of the torques should be equal to 0 in order to find the tipping point around either of the wheels.

My problem is with the 1000N applied at to top taking the pivot point around the left wheel.

Should I be using the component of the 1000N which is at right angles to the distance to the pivot point? (the green line) and take the green line as the distance? should I use 'h' as the distance to the pivot point with 1000N as the force? or a combination of both?

The same for m*g in the diagram. Should I assume that the centre of mass is where the weight is applied and take the perpendicular component?

Thanks very much for your help guys! Been a long time since I looked into this.

 

[jack action]

By definition, the torque is the result of a cross product of 2 vectors, i.e. $\mathbf{T} = \mathbf{r} \times \mathbf{F}$. The magnitude of this torque (what you are looking for) is $T = rF\sin\theta$ where $\theta$ is the angle between the 2 vectors. This basically means that only the components of the vectors that are perpendicular to each other are considered.

You can see it as $r_{\perp} F$ or $r F_{\perp}$ as you wish, since both will give you the same answer: $rF\sin\theta$.

The following is a representation of $r F_{\perp}$:

The following is a representation of $r_{\perp} F$:

So in your case, you take 1000 N times h ( or $r_{\perp} F$). You could use $r F_{\perp}$ by using the length of the green line and by finding the perpendicular component of the 1000 N force (the orange line), it would give the same answer. It is just more complicated in this particular case.

Similarly, for the weight, you take mg times x₂. Where x₂ is the perpendicular component of the distance between the wheel and the center of mass.

 

[DarkBlitz]

Thanks a lot! cleared it up!