- #1
TheTraceur
- 2
- 0
Hi everyone! I'm not very good at math as I'm in high school, and so probably did something wrong in this, but I did some calculations and am now wondering if a flat Universe requires Ω0 ≠ 1?
I started with the Friedmann equation,

If you divide by 3 and take the inverse of both sides, you get,
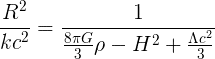
Since,
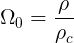
Where ρc is the critical density, we can re-write the equation in terms of Omega (I also multiplied both sides by c2),

Here it to me looks a bit odd, because here Omega being one does not correspond to a Universe with infinite radius of curvature, since you still have to cosmological constant, which is positive. Here it seems that if you want to assume that k = 0, and so have a flat Universe, you will need to have (since if R2/k, where k = 0, is 'infinite', then the other side must also be 'infinite'):


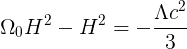
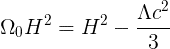
We then get:
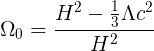
And since the cosmological constant has been discovered to be positive, this would seem to mean that for a flat Universe (k = 0), Ω0 is not exactly equal to one, but in fact a tiny bit smaller. I'm pretty sure this is false, but I don't know where I've missed the fault in the derivation. May it be that the cosmological constant is assumed to be zero in the definition of critical density? Because if you don't assume a zero value for the cosmological constant in the definition of critical density, the cosmological constant dissapears in the denominator, and so Omega being one corresponds to a flat Universe.
I started with the Friedmann equation,
If you divide by 3 and take the inverse of both sides, you get,
Since,
Where ρc is the critical density, we can re-write the equation in terms of Omega (I also multiplied both sides by c2),
Here it to me looks a bit odd, because here Omega being one does not correspond to a Universe with infinite radius of curvature, since you still have to cosmological constant, which is positive. Here it seems that if you want to assume that k = 0, and so have a flat Universe, you will need to have (since if R2/k, where k = 0, is 'infinite', then the other side must also be 'infinite'):
We then get:
And since the cosmological constant has been discovered to be positive, this would seem to mean that for a flat Universe (k = 0), Ω0 is not exactly equal to one, but in fact a tiny bit smaller. I'm pretty sure this is false, but I don't know where I've missed the fault in the derivation. May it be that the cosmological constant is assumed to be zero in the definition of critical density? Because if you don't assume a zero value for the cosmological constant in the definition of critical density, the cosmological constant dissapears in the denominator, and so Omega being one corresponds to a flat Universe.
Last edited: