On the derivation of Child-Langmuir law

[elgen]

This problem is from Griffiths' book Introduction to Electrodynamics [Problem 2.53 in 4th edition].

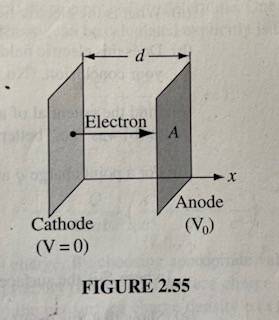
It considers that electrons are emitted from the cathode and move to the anode. This establishes a constant current between the parallel plates. It asks to show that the constant current $I$ and the potential difference $V_0$ have this relation $I\propto V_0^{\frac{3}{2}}$, the Child-Langmuir law.

I started with Poisson's equation
$$\frac{d^2 V}{dx^2} =- \frac{\rho}{\epsilon_0}$$
The relation among the current $I$, the charge density $\rho$, and electron speed $v$ is
$$I = A \rho v$$
where $A$ is the plate area. My understanding is that
$$v=\sqrt{\frac{2x}{m}(-\frac{dV}{dx}q)}$$
where $m$ is the electron mass and $q$ denotes the charge. This leads to the following DE
$$\frac{d^2 V}{dx^2} =- \frac{I}{\epsilon_0 A \sqrt{\frac{2x}{m}(-\frac{dV}{dx}q)}}$$
which I do not know how to proceed to solve for $V$.

In the meanwhile, I suspect that I need to use $-\frac{dV}{dx}=V_0/d$ on the RHS of Poisson's equation. This leads to
$$V=-\alpha\frac{4}{3}x^{3/2}+\frac{V_0+\alpha\frac{4}{3}d^{3/2}}{d}x$$
where $\alpha=\frac{I}{\epsilon_0 A \sqrt{2V_0q/md}}$, and
$$-\frac{dV}{dx}=\alpha 2 x^{1/2}-(V_0+\alpha\frac{4}{3}d^{\frac{3}{2}})/d$$.
Wouldn't this contradict to assumption of $-\frac{dV}{dx}=V_0/d$? I am confused. Any comments on this derivation is appreciated.

 

[anuttarasammyak]

My understanding is that
v=2xm(−dVdxq)
where m is the electron mass and q denotes the charge.

\frac{1}{2}mv^2=qV
isn't it though sign of q,V are to be investigated carefully ?

 

[elgen]

Thank you for the pointer.

$q$ is the electron charge, so it is negative. To have a positive kinetic energy, $V$ is negative, no? This does not feel right, as I would expect $V$ to remain positive between the plates.

In the meanwhile, when I wrote v=\sqrt{2x/m(-dV/dx)q, I wrongly assumed a constant electron acceleration. From the energy relation, Poisson's equation becomes
$$\frac{d^2V}{dx^2}=-\frac{I}{\epsilon_0 A\sqrt{\frac{2q}{m} V}}$$
which does not yield a solution in terms of elementary functions. What else is missing here?

 

[vanhees71]

Nothing is missing here except the solution of the differential equation. Hint: Multiply with $\mathrm{d} V/\mathrm{d} x$ for a first integral!

 

[elgen]

Thank you. I got $$V=V_0(x/d)^{\frac{4}{3}}$$ and $$I=\frac{-4\epsilon_0 A}{9d^2}\sqrt{\frac{2q}{m}}V_0^{\frac{3}{2}}$$

 

[Delta2]

Is there a way to prove that the current $I$ is independent of time $t$ and position $x$ or we just take it as a fact because that's what the experiment tell us?

 

[elgen]

The constant current is given as an experiment result.