One-dimensional Uniform plane wave

[avinamaurya]

to solve one dimensional uniform plane wave, why assumed E = F1(z-ct) + F2(z+ct) as a general solution of second order differential equation and in trigonometric form particular function assumed to be Ey =Sin B(z+mt).. Is there any other method like Laplace solution or something where i don't have to assume this... ..

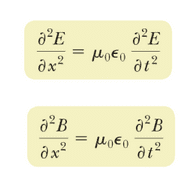
Is there solution exist without assuming anything for this function.

 

[vanhees71]

Let's write the equation as
$$\partial_1^2 f(x_1,x_2)-\partial_2^2 f(x_1,x_2)=0.$$
You can always set $x_1=c t$ to get it in physical units of time.

This is the wave equation in 1 spatial dimension. Now the trick is to rewrite this in terms of "light-cone coordinates",
$$\xi=x_1+x_2, \quad \eta=x_1-x_2.$$
Now you have, according to the chain rule,
$$\frac{\partial}{\partial x_1} f=\frac{\partial \xi}{\partial x_1} \frac{\partial f}{\partial \xi} +\frac{\partial \eta}{\partial x_1} \frac{\partial f}{\partial \eta}=\frac{\partial f}{\partial \xi} + \frac{\partial f}{\partial \eta}.$$
In the same way you derive step by step the second derivatives $\partial_1^2$ and $\partial_2^2$ in terms of the derivatives with respect to the light-cone variables $\xi$ and $\eta$.

At the end the wave equation reads
$$\partial_{\xi} \partial_{\eta} f=0.$$
This is now very easy to integrate. The vanishing of the partial derivative with respect to $\xi$ means that the function is only dependent on $\eta$. Thus you have
$$\partial_{\eta} f=g(\eta).$$
But this implies that
$$f(\xi,\eta)=f_1(\eta)+f_2(\xi), \quad f(\eta)=\int \mathrm{d} \eta g(\eta).$$
There's an additional function $f_2(\xi)$, because the partial derivative of a function wrt. to $\eta$ determines this function only up to a function, indepenent of $\eta$, i.e., it can only depend on $\xi$.

Now you can rewrite this equation in terms of the old coordinates, i.e.,
$$f(x_1,x_2)=f_1(x_1-x_2) + f_2(x_1+x_2).$$
Here $f_1$ and $f_2$ are indeed arbitrary functions that are determined by appropriate initial and boundary conditions.