- #1
Tyto alba
- 62
- 0
I want to study chi square test of homogeneity from any authentic source- book / website especially problems where samples are compared for more than one attribute.
What are some relevant sources?
Relevant background:
I was studying examples from random online sources before I saw this book in which a second X2
has been calculated and has been substracted from the principle X
2 (the one we usually find). This is inconsistent to the examples I saw online.

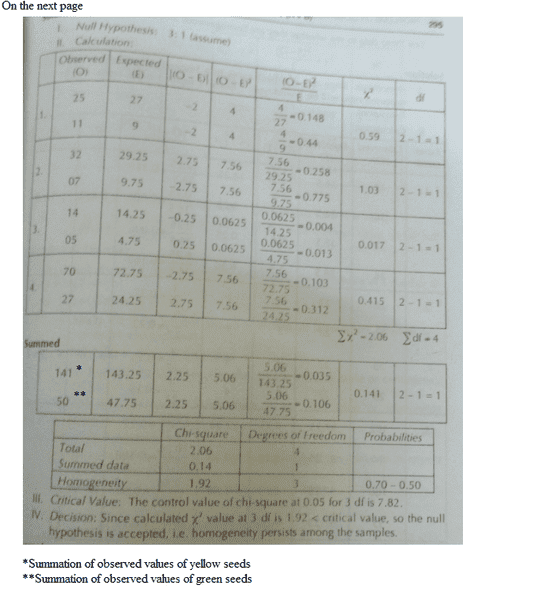
Infact we are being taught the latter process.
Chi square test of homogeneity is a Chi square test that determines whether two or more independent random samples are from the same or different population.
What are some relevant sources?
Relevant background:
I was studying examples from random online sources before I saw this book in which a second X2
has been calculated and has been substracted from the principle X
2 (the one we usually find). This is inconsistent to the examples I saw online.
Infact we are being taught the latter process.