altruan23
- 22
- 5
- Homework Statement
- Calculate Uout/Uin
- Relevant Equations
- Basic op amp eq.
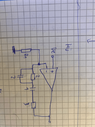
So this is the circuit.

And here i tried to calculate Uout/ Uin , any suggestion how to simplify this term?? I used Uout= Uin * (1+ Z2/Z1)
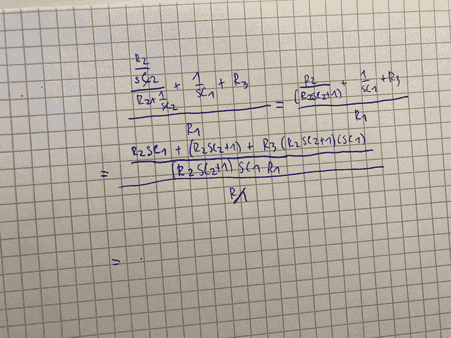
And here i tried to calculate Uout/ Uin , any suggestion how to simplify this term?? I used Uout= Uin * (1+ Z2/Z1)